NEW DIRECTIONS IN RESEARCH ON LANGUAGE DEVELOPMENT
ELIZABETH BATES
University of California, San Diego
AND
GEORGE F. CARNEVALE
Scripps Institution of Oceanography
[webmaster note: Some of the equations in this paper
are impossible to reproduce with the current version of HTML. Attempts will
be made in the future to take advantage of HTML extensions that will enable
super- and subscripts.]
Forecasting is a thankless task. The U.S. Weather Bureau figured that out
a number of years ago. When we were children1,
the weathermen used to pore over their statistics and come up with a 'yes'
or 'no' decision: "It will rain tomorrow". In today's world, the
statistics are passed on to us directly, unadorned: "There is a 40%
probability of rain tomorrow". If you want to organize a picnic based
on those statistics, it's your problem. In this paper, we are going to take
the same conservative strategy. We will describe what are, in our view,
the newest and most exciting trends in current research on language development,
and assume (hope) that these are the trends that will predominate in the
few years that remain until the millenium. The paper is organized into six
sections: (1) advances in data sharing, (2) improved description and quantification
of the linguistic data to which children are exposed, and the data that
they produce; (3) new theories of learning in neural networks that challenge
old assumptions about the "learnability" (or unlearnability) of
language, (4) increased understanding of the non-linear dynamics that may
underlie behavioral change, (5) research on the neural correlates of language
learning, and (6) an increased understanding of the social factors that
influence normal and abnormal language development.
(1) Data sharing
In contrast with some of the sections that follow, what we have to say here
is surely uncontroversial: Any field profits immensely when investigators
are willing to pool their efforts, sharing data and other resources for
the common good. In the field of child language, there have been some very
healthy trends in this direction in the last five years, with important
implications for the way that research will be done for the foreseeable
future. We will concentrate here on two compelling examples of successful
collaboration on a large scale: the Child Language Data Exchange System,
and the MacArthur Communicative Development Inventories. We present these
examples in some detail (and brag at length) in the hope that other examples
of the same quality will follow, setting a very positive trend for the 1990's.
The Child Language Data Exchange System (ChiLDES):
The Child Language Data Exchange System (ChiLDES) was founded in 1984 by
Brian Mac-Whinney and Catherine Snow, at an organizational meeting in Concord,
Massachusetts, attended by many of the most important figures in child language
research (MacWhinney and Snow, 1985). The need for such a system was clear,
but it was less obvious how to meet that need. Longitudinal studies of language
develop-ment have played a major role in the modern history of this field,
with a primary focus on samples of free speech in naturalistic situations.
But a single hour of free-speech data typically involves 10 to 40 hours
of transcription and coding, depending on the interests of the investigator.
In other words, this is an expensive and labor-intensive enterprise. And
yet, prior to the foundation of ChiLDES, free-speech transcripts were gathered
separately by each team of investigators, milked of their value for that
particular project, and left to molder on laboratory shelves. Investigators
in the field had long recognized the wastefulness of this practice, since
any single sample of free-speech data can have multiple uses that were never
envisioned by the researcher who gathered those data in the first place.
But there was no obvious way to centralize hard copies of free-speech data
while preserving access to scientists from many different institutions.
By the early 1980's, it was clear that microprocessor technology could be
used to resolve this problem, creating a living archive with the potential
for immediate electronic access and inexpensive duplication. The idea of
such an archive was conceived independently in the early 1980's by investigators
at several different institutions (e.g., Harvard, Berkeley, Carnegie Mellon,
and the Max Planck Psycholinguistics Institute), but no one had the necessary
resources to get such an enterprise off the ground.
In 1983, MacWhinney and Snow submitted a proposal to the MacArthur Foundation
(sponsored by the Early Childhood Transitions Network) for a computerized
child language data exchange system. The Foundation provided substantial
funding in the first years of the project, while MacWhinney and his colleagues
provided a great deal of hard work and ingenuity to solve the myriad technical,
legal, social and scientific problems that were involved in making ChiLDES
work. One of the most important contri-butions was CHAT, a complex but flexible
multi-tiered coding scheme for computerized free-speech transcripts. Prior
to the development of CHAT, each investigator made independent and often
idiosyncratic decisions about the format for coding free speech (e.g., what
to leave out and what to keep, what symbols to use, how to evaluate and
count "speech errors" of different kinds). Establishment of a
common archive has meant that child language researchers have had to pool
their knowledge and experience to develop a common set of coding decisions.
CHAT developed iteratively across a 5 - 6 year period, as investigators
from all over the world pointed out new problems and made new recommendations
for this first-ever universal language coding system. The manual itself
is now the size of a telephone directory for a mid-sized city, and has just
been published as a book by Erlbaum Press (MacWhinney, 1991). Another important
contribution is CLAN, a set of procedures for the automated analysis of
language transcripts; CLAN software is (like use of ChiLDES itself) free
of charge to any scientist who agrees to respect the ChiLDES guidelines
(e.g., protection of confidentiality, proper citation of original sources,
return of new results and new analyses to the ChiLDES system itself).
The MacArthur Foundation's responsibility for ChiLDES ended around 1988.
Since that time, MacWhinney and Snow have kept the enterprise going entirely
through independent funding from the National Science Foundation and the
National Institutes of Health. The latter includes a large grant from NICHD
called "Foundations of language assessment", to solve new problems
in data analysis and to extend these analytic tools to a range of clinical
populations. In addition, investigators in other countries (e.g., Italy,
Denmark) have obtained funding from their governments to prepare data in
their language for contribution to the ChiLDES system. The CHAT and CLAN
procedures have also figured prominently in many individual grant proposals,
and it is now quite common for scientists to promise contribution of their
data base to ChiLDES as an important selling point in their efforts to obtain
funding. A small group of investigators in neurolinguistics have now established
an analogue called ALDES (Aphasic Language Data Exchange System), a system
that is "piggybacked" onto ChiLDES, profiting from all the technical,
legal, social and scientific innovations that ChiLDES has provided.
But the most important outcome has been the impact of a large shared data
base on scientific activity within the field of developmental psycholinguistics.
When MacWhinney and Snow submitted their last proposal for renewal of the
NIH grant (a proposal that met with considerable success), they were able
to cite no fewer than 250 books, journal articles, chapters, conference
proceedings and conference presentations based wholly or partly on the ChiLDES
data base. To be sure, a system for sharing old data is no substitute for
new experiments and new forms of data collection. But the data exchange
system has several uses that greatly enhance the quality of new scientific
activity: (1) new hypotheses can be checked against existing data and refined
prior to the launching of an expensive new research project; (2) data from
several different projects can be pooled to provide the necessary power
to test hypotheses that cannot be evaluated with a small sample; (3) novice
researchers can use the existing data base to learn about the general properties
of child speech, before they are "set loose" on real live children;
(4) researchers in fields like artificial intelligence and neural modelling
(i.e. researchers who have no other access to "real" child language)
have used ChiLDES data to model aspects of the language learning process;
(5) in the process of developing a common coding system, researchers have
become aware of the theoretical assumptions behind each individual coding
decision; as a result, communications in our field have improved and our
methodology is far stronger and more explicit than it was before ChiLDES
was founded.
The MacArthur Communicative Development Inventories (CDI):
Another example of successful large-scale collaboration in our field comes
from the development of a new parental report instrument for the early stages
of lexical and grammatical development, the MacArthur Communicative Development
Inventories, known as the CDI (Fenson, Dale, Reznick, Thal, Bates, Hartung,
Pethick and Reilly, 1993). Here too, a group of researchers has responded
to a widespread need in our field, coming up with a solution that would
be beyond the means of any individual laboratory.
The earliest stages of language learning are difficult to observe, because
the behaviors in question are new, infrequent, and unpredictable. The most
valid and reliable information comes from observers who are with the child
all the time, i.e. the child's own parents. For this reason, diary studies
by the parent/scientist have been central to our understanding of developments
in the period from 8 - 30 months (e.g., Dromi, 1987). Needless to say, such
studies are few and far between, and it is difficult to generalize from
case studies of privileged academic infants to the range of variability
that we might expect across the normal population. To develop solid norms
for early language development, we had to find a way to "bottle"
the diary study and administer it on a very large scale.
For more than fifteen years, researchers have been developing a parental
report instrument that taps into the parents' wealth of knowledge about
their child's burgeoning linguistic abilities (Bates, Camaioni and Volterra,
1975; Bates, 1979; Shore, O'Connell and Bates, 1984; Shore, 1986; Reznick
and Goldsmith, 1989). At first, this instrument was developed and applied
on a very small scale, as we learned how to obtain valid and reliable data
from parents. For example, we learned how to get around the parent's natural
pride and lack of expertise by asking only about current behaviors (retrospective
report has proven very unreliable), asking only about behaviors that are
just starting to happen (so that a parent has a reasonable chance to keep
track), and asking questions in a form that avoids the need for interpretation
and draws on the power of recognition memory (e.g., "Does your child
say 'tiger'?" as opposed to "what animal words does your child
say?"). When these criteria are followed, parental reports of language
development have proven valid and reliable.
A final version of this instrument has been produced by Larry Fenson and
colleagues, with support from the MacArthur Foundation (Fenson et al., 1993).
This version comes in two parts: the Infant Scale (which examines word comprehension,
word produc-tion, and aspects of symbolic and communicative gesture, in
the period from 8 - 16 months) and the Toddler Scale (which looks at word
production and the early phases of grammar, in the period from 16 - 30 months).
Normative data have been gathered from more than 1,800 normally developing
children, in three different cities (San Diego, Seattle, New Haven). For
approximately one third of the sample, a longitudinal follow-up was also
obtained (at a one-month interval for children in New Haven; at a six-month
interval for children in San Diego and Seattle). For subsamples of the children
at each site, the team also conducted a series of small "validation
modules", to insure that the same high correlations between parental
report and laboratory observations obtained in earlier studies had been
preserved in the new and final version of the instrument (Dale, Bates, Reznick
and Morisset, 1989; Dale, 1990 and 1991; Fenson, Thal and Bates, 1990; Jackson-Maldonado,
1990). So far, all these validation studies provided solid evidence that
the CDI reflects real and observable events in early language develop-ment.
For example, the word production checklist correlates with laboratory observations
of vocabulary in a range from +.60 to +.80 depending on the study. The grammar
scale works just as well, if not better, correlating with Mean Length of
Utterance (the single best laboratory index of grammatical complexity at
this point in development) in a range from +.75 (at 24 months) to +.82 (at
20 months). In addition, the internal reliability of both scales has proven
to be extraordinarily high, with split-half correlations averaging +.95
- +.99.. These validity and reliability figures are comparable to results
obtained with well-known instruments like the Stanford Binet Adult Intelligence
Scale.
The norming study has provided a wealth of information in its own right,
on the shape and nature of the first words and first sentences children
use, on the range of variability that can be observed in healthy children
from 8 - 30 months, on the contribution (or non-contribution) of demographic
factors to early language development (e.g., sex differences are real, but
they are much smaller than previously believed), and on the relationship
between vocabulary development and the emergence of grammar (i.e. grammar
appears to be tightly linked to word learning, above and beyond the general
effects of age and maturation shared by these two linguistic domains). These
data have already helped to decide between alternative hypotheses about
the emergence of language, and they have provided absolutely compelling
evidence about normal variation. In addition, clinicians now have tools
to determine what really constitutes a "late talker", and several
clinical studies have already shown that the CDI can be used as early as
18 months of age to identify children who are at risk for specific language
impairment (Thal and Bates, 1988; Thal, Tobias and Morrison, 1991).
This simple low-cost instrument is beginning to have a broad impact; in
the three years since Fenson et al. first began to make the instrument available
to colleagues in the field (on a non-profit basis), they have sent out more
than 17,000 copies of the instrument. For example, the CDI will be a central
instrument for the evaluation of language development in a Pittsburgh University
Medical Center study of otitis media (involving more than 6,000 children),
and it will be a major outcome variable in a NIH-funded collaborative study
of day care vs. home care at ten different research sites across the country.
Philip Dale and Larry Fenson have also established a CDI data base, to centralize
information from different normal and abnormal populations. It seems clear
that they have met a huge need, in clinical as well as research settings,
for a cost-effective but highly reliable and valid tool for the assessment
of early language development. Not surprisingly, colleagues in other countries
have already begun to develop adaptations of the CDI for their own language,
and versions are now available in Italian (Camaioni, Caselli, Longobardi
and Volterra, 1991), Spanish (Jackson-Maldonado, 1990; Jackson-Mal-donado,
Marchman, Thal, Bates, and Gutierrez-Clellen, in press; Japanese (Ogura,
1991) and American Sign Language (Reilly, 1992).
(2) Quantification of linguistic input and output
Because of ChiLDES and related large-scale efforts at data sharing, our
field is now in a much better position to describe and quantify linguistic
behavior - including the language produced by children, and the linguistic
input to which children are exposed in different language communities, at
different points in development. Indeed, one might well ask how we managed
before such tools were at our disposal.
The answer lies, at least in part, in a series of old assumptions about
the nature of language development. Until recently, most researchers in
this field have viewed language learning in purely qualitative terms, as
a kind of theory-building process in which children test alternative hypotheses
about their grammar in a "yes-no" fashion. In some theories, it
is further assumed that these hypotheses are innate, and relatively explicit
(e.g., the "parameter-setting" approach - Hyams, 1986; Roeper
and Williams, 1987). In other theories, the suggestion has been made that
children derive hypotheses about their grammar from aspects of non-linguistic
cognition (e.g., postulation of a rule for agent-action mapping - Braine,
1976; Bowerman, 1973). From either perspective, it is usually assumed that
quantitative factors like type and token frequency play a minimal role (e.g.,
Brown, 1973; Pinker, 1981). Indeed, some researchers have gone so far as
to suggest that language development can take place in the absence of any
input at all (Goldin-Meadow and Mylander, 1985; Crain, 1992). Whether or
not they embrace this radical nativist view, developmental psycholinguists
have been skeptical about the need for a precise statistical characterization
of the child's linguistic output and/or the linguistic environment.
There is of course one sure-fire way to guarantee the failure of a quantitative
approach to language learning: quantify things badly, and show thereby that
statistical effects do not matter. For example, Brown and Hanlon (1970)
studied the linguistic environment of one child, Adam, and claimed that
his parents rarely provided any explicit negative feedback about the grammaticality
of the child's speech (i.e., they rarely corrected the child, and rarely
rephrased incorrect utterances into a correct form). Many students of language
development cite the results of this small study as definitive evidence
that children do not receive negative evidence (Pinker, 1984; Bohannon and
Stanowicz, 1988; Bohannon, MacWhinney and Snow, 1990; Sokolov and Snow,
1992), a claim with important theoretical repercussions (see section 3,
below). Of course Brown and Hanlon cannot be held responsible for this overgeneralization
of their results. The responsibility rests on the shoulders of those who
assume that one case study (with limited quantification, and a limited definition
of "feedback") can settle an issue of this magnitude for all time.
With the increased precision that is now available (thanks in part to the
ChiLDES data base), a number of researchers have now shown that a great
deal of implicit negative evidence is present in the data to which children
are exposed, including contingent partial repetitions that occur several
utterances "downstream" from the child's initial error (Bohannon
and Hirsh-Pasek, 1984; Sokolov and MacWhinney, 1990). In fact, they have
shown these effects within the very data base that Brown and Hanlon used
in the early 1960's.
This is not the only example of its kind. There are a number of instances
in the last few years in which results of an earlier study have been turned
around entirely by a more thorough and sophisticated quantification of the
same data base. For example, Hyams (1986) examined isolated sentences from
secondary sources on English, German and Italian child language, and drew
some very powerful conclusions about "sudden" changes in linguistic
output based on setting of innate parameters. Since publication of this
interesting and provocative work, researchers in each of these language
groups have put Hyams' ideas to a more rigorous test, returning to the language
transcripts that were used to generate the secondary sources on which Hyams
based her conclusions (for English, see O'Grady, Peters and Masterson, 1989;
Loeb and Leonard, 1988; Radford, 1990; for German, see Jordens, 1990; for
Italian, see Valian, 1990 and 1991; Pizzuto and Caselli, in press). In virtually
every case, her initial conclusions have been rejected in favor of a more
gradual form of "garden variety" learning.
But what exactly is "garden variety learning"? The role of input
statistics in language development depends crucially on the theory of learning
that we set out to test (an issue to which we shall turn shortly). At this
point, we simply want to emphasize that the field of child language has
reached a new level of precision and sophistication in the way that we code
and quantify linguistic data. Single-case studies, qualitative descriptions
and compelling anecdotes will continue to play an important role. But they
cannot and will not be forced to bear the full weight of theory-building
in our field.
(3) Learning, learnability and neural networks
One of the most influential movements in child language research throughout
the 1980's was an enterprise called Learnability Theory (Wexler and Culicover,
1980; Pinker, 1979; Baker 1981). This line of research is actually a branch
of computational linguistics, and in many cases it is practiced without
any direct use of behavioral data from real human children. Instead, the
field has grown up in response to a logical problem, called Baker's Paradox:
How can children recover from errors of overgeneralization (e.g., "goed",
"stooded up") when nobody tells them that they are wrong? In a
much-cited paper within computational linguistics, Gold (1967) provided
a formal proof showing that grammars of a certain complexity (i.e. context-sensitive
grammars, a class to which natural languages supposedly belong) could not
be learned by an hypothesis-testing device that is exposed only to positive
evidence (i.e. examples of sentences that are possible in the grammar),
without negative evidence (i.e. examples of sentences that are not possible
in the grammar). This finding was presented as a formal proof, but it can
be paraphrased in common-sense terms: Even if an hypothesis-testing device
were to "guess" the right grammar (G) at some point in learning,
it would have no way of knowing that it was right. It might go on to guess
a bigger grammar (G + 1), containing sentence types that are not permitted
in G. In the absence of negative evidence, the machine is playing a guessing
game of the "Hot and Cold" type in which the data tell it "You're
getting warmer" without ever providing information of the opposite
sort (i.e. "You're getting colder"). The argument is similar to
a broader argument against the possibility of inductive learning raised
by Nelson Goodman (1979).
There are only a few ways out of the learnability paradox: (1) assume that
negative evidence is available in some form; (2) relax the criteria used
to evaluate when learning is complete (e.g., if the right grammar is "G"
and the system guessed "G + 1" or even "G - 1", call
it "Close enough for Government work"); (3) provide the system
with enough prior knowledge to rule out impossible grammars and zero in
on a finite set of possible grammars. For the reasons outlined above (i.e.
the Brown and Hanlon study), most researchers working within the learnability
paradigm assume that negative evidence is not available to real human children.
They also argue that a relaxation of success criteria flies in the face
of what we know about the nature of adult linguistic knowledge (i.e. an
abstract set of crisp and discrete rules that go well beyond the data to
which children are exposed). That leaves only one solution: Assume that
a great deal of innate knowledge is available.
From this point of view, learnability analysis can be viewed as a kind of
equation, in which values are assumed for three important factors on the
left-hand side of the equation: the nature of the target grammar (i.e. the
knowledge that has to be learned), the nature of the learning device, and
the nature of the data set to which that device is exposed. The right-hand
side of the equation is the amount and kind of innate knowledge that we
have to assume for learning to go through, under the assumptions (values)
assigned on the left. The left side of Table 1 illustrates the assumptions
that are usually made by learnability theorists working within the field
of child language. First, they assume (following Gold) that the target grammar
consists of a set of abstract rules applied to strings of discrete symbols,
generating all possible sentences (and no impossible sentences) in the target
language. Second, they assume that the learning device itself is an hypothesis-testing
device that "guesses" a whole grammar (and/or an individual rule
in that grammar) and tests it against a succession of input strings until
it is ruled out (i.e. until a string is encountered that cannot be accounted
for by the grammar that is currently under consideration). Note that the
grammar itself is made up of discrete entities, and the decision process
applied by the learning device is equally discrete. That is, a candidate
rule or set of rules are accepted, or rejected, in a yes-no fashion. Obviously
there is little room for error with a brittle learning device of this kind;
a little bit of bad data or an off-course search through the space of possible
grammars could derail the system forever. Finally, they assume that the
linguistic input is limited to positive evidence, and they often make the
further assumption that this positive evidence isn't very good. At best
it underrepresents the range of sentence types available in the grammar;
at worst, it is faulty and error-prone, so that it actually misrepresents
the range of possible sentences that the grammar would permit. Given these
assumptions - an abstract grammar that must be learned by a brittle hypothesis-testing
device, with a faulty and limited data base - an extensive amount of innate
knowledge must be assumed for learning to go through.
TABLE 1:
ALTERNATIVE ASSUMPTIONS AND SOLUTIONS TO THE PROBLEM OF LANGUAGE LEARNABILITY
STRONG VERSION WEAK VERSION
1. TARGET GRAMMAR: A SYSTEM OF DISCRETE RULES SYSTEM OF WEIGHTED
AND/OR PRINCIPLES OPERATING FORM-FUNCTION MAPPINGS
OVER STRINGS OF DISCRETE
SYMBOLS
2. DATA BASE: --POSITIVE DATA --POSITIVE DATA
--UNDERDETERMINED --UNDERDETERMINED
--UNSYSTEMATIC --UNSYSTEMATIC
3. LEARNING DEVICE: DISCRETE 'YES/NO' DEVICE THAT --ROBUST PROBABILITY SAMPLER
TESTS WHOLE GRAMMARS AND/OR --N-LAYER CONNECTION SPACE
INDIVIDUAL RULES ONE AT A TIME --NON-LINEAR DYNAMICS
AGAINST EACH INPUT STRING
_______________________________ ________________________________
4. AMOUNT OF PRIOR HIGH LOW
KNOWLEDGE
REQUIRED FOR
LEARNING:
The right side of Table 1 shows that a different conclusion can be reached
if we change some of the values on the left-hand side of the equation. Suppose,
for example, that we assume a different kind of learning device: Instead
of a brittle hypothesis-testing device that reaches "yes/no" conclusions,
one at a time, we assume a device that samples probabilistically from the
input strings. Although this doesn't solve the problem completely, a probabilistic
device of this kind would be much less error prone; it draws its conclusions
from the "solid" regions of the input space, and cannot be thrown
off too far by a little bit of bad data. Suppose, in addition, that we assume
a different kind of target grammar: Instead of a list of absolute rules
over discrete symbols, we assume that the target grammar consists of a set
of probabilistic mappings between form and meaning. Under these more plastic
assumptions (i.e. a "rough and ready" learning device and a target
with fuzzier boundaries), we end up with a less stringent definition of
learning itself, where "success" is also defined in approximate
terms (i.e. "close enough for Government work"). In short, by
turning a discrete and absolute definition of learning into a stochastic
process, learnability may be possible with far fewer assumptions about innate
knowledge (i.e. with far less "stuff" on the right-hand side of
the equation).
But there are even more radical ways to turn the learnability problem around,
a qualitatively different approach to learning that involves much more than
a relaxation (lowering?) of standards. Let us illustrate this point with
a metaphor. Figure 1a displays a daunting array of arrows pointing in different
directions. Assume that all these arrows represent a set of possible paths.
The learner's problem is to uncover the "right" path, i.e. the
overall direction that it ought to take based on all this information. Which
one is the "right" arrow? Imagine the poor learner forced to sample
these "possible arrows" one at a time, with no information about
"impossible arrows"? Figure 1b shows that same situation, with
more data. Obviously more data does not help! It only makes the problem
worse. Under the assumption that learning consists solely of "sampling
arrows one at a time", it should be clear why no conclusion can ever
be reached.
Suppose, however, that the same information is evaluated in a different
way, applying an operation called vector addition. A vector is a
mathematical entity that expresses two aspects of a single movement through
some hypothetical space: direction and distance. Each of the arrows in Figures
1a and 1b illustrates an individual vector in a two-dimensional space. Whenever
two vectors are added together, the result is another vector, i.e. a single
movement through the same space (Movement C) that refects the combined effect
(in distance and direction) of carrying out both Movement A and Movement
B. An illustration is provided in Figure 1c. As it turns out, the multitude
of arrows in Figures 1a and 1b contain a robust and significant generalization,
if those arrows (or some representative subset of those arrows) are combined
through vector addition. Figure 1d illustrates the "mega-arrow"
that would result by applying vector addition to the "data" in
Figures 1a and b. This result is certainly not obvious to the naked eye,
much less to the poor one-at-a-time-sampler-of-arrows. But it is there,
in the data set as a whole and in any robust and representative subsample
of those data.
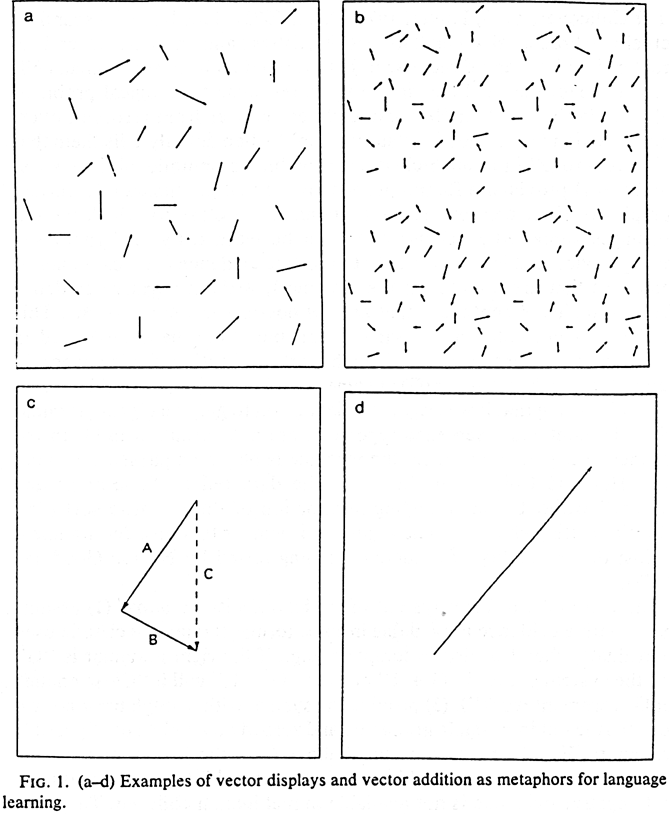
Language learning is not the same thing as vector addition. This is,
after all, a parable. The main point is that the same stimulus set may be
impoverished or very rich, depending on the techniques used to explore it.
Forms of learning that are impossible in one framework may be quite plausible
in another - which brings us to the main point of this particular section,
the availability of a new paradigm for the study of learning that has great
potential for our understanding of language development.
As we have already pointed out, the learning device assumed by most investigators
working within the Learnability framework is a limited, brittle and highly
unrealistic device. But for approximately thirty years of research in language
development, that has been the only learning device under consideration
- which is tantamount to saying that thirty years of research on language
acquisition have been carried out in the absence of a theory of learning
per se. Indeed, some investigators have denied that learning is at all relevant
to language development, a position that is well illustrated by the following
quote from Piatelli-Palmarini (1989, p. 2):
"I, for one, see no advantage in the preservation
of the term learning. We agree with those who maintain that we would gain
in clarity if the scientific use of the term were simply discontinued..."
Fortunately for those of us who cling to a stubborn interest in learning
and change, Piatelli-Palmarini's recommendations have not been followed.
Instead, the 1980's witnessed some dramatic developments in our understanding
of the learning process, based on a radically different form of computer
architecture than the standard serial digital computer that has dominated
our view of the mind since the 1950's (for a detailed discussion, see Bates
and Elman, 1993). This new approach goes under several names, including
Parallel Distributed Processing (Rumelhart and McClelland, 1986), Connectionism
(Hinton and Shallice, 1989; Bates and Elman, 1993) and/or Neural Networks
(Churchland and Sejnowski, 1992). A full review of connectionism is well
beyond the scope of this small paper, but a few words about the difference
between traditional computer models of learning and the new connectionism
paradigm may be useful.
In traditional computer models, knowledge is equated with a set of programs.
These programs consist of discrete symbols, and a set of absolute rules
that apply to those symbols. By "discrete" we mean that a symbol
is either present, or absent; there is no such thing as 50% of a symbol.
By "absolute", we mean that a rule always applies when its conditions
are met; there is no such thing as 25% of a rule. Under these assumptions,
it is very difficult to conceive of a way that the system could "settle
in" to an approximation of a target grammar. Furthermore, in traditional
computer models the knowledge (software) is physically and logically separate
from the processor itself (hardware). Programs have to be retrieved, loaded
up into some short-term processor, and then put back where they came from.
The program itself is executed, one step at a time, by a single Executive
Processor. This assumption of seriality would result in a serious "bottleneck"
on processing, if it were not for the fact that modern computers are so
very fast - much faster, in fact, than the time it takes for a single piece
of information to move from place to place in the human brain. Finally -
and this is the most important point for our purposes here - there are only
two ways that learning can take place in a traditional computer model: programming,
or hypothesis-testing. In learning-by-programming, someone or something
has to put the knowledge directly into the computer by hand. In learning-by-hypothesis-testing,
possibilities that were already there in the program (i.e. "innate"
hypotheses) are accepted or rejected, depending on their fit to the data.
In other words, nothing really new can happen if we assume that the mind
is like a serial, digital computer: Either the knowledge is already there
in the machine, or the knowledge is already there outside the machine in
the form of a computer program.
Connectionism is based on a very different metaphor for mind and brain,
a computational device called the Connection Machine. This device consists
of a large number of highly interconnected units that operate locally but
converge in parallel to solve problems and extract invariant cues from a
highly variable environment. These systems are important for developmental
psychology for several reasons. First, they are self-organizing systems;
that is, they change and learn in ways that are not directly controlled
by an experimenter/programmer, and they can be used to discover properties
of the input that experimenters did not see before the simulation was underway.
Second, they are non-linear dynamic systems; their behavior is not fully
predictable, and they often display sudden and unexpected changes in behavior
of the kind that we so often witness in children and adults (see below).
Third, they are "neurally inspired", brain-like systems; as such,
they provide a new level of analysis midway between brain and behavior,
promoting new forms of collaboration between behavioral scientists and neuroscientists
with a common interest in learning and development. The connectionist movement
has taken cognitive science, computer science and neuroscience by storm,
and it has returned the issues of learning and change back to center stage
in all these fields. The movement has great potential for the field of develop-mental
psychology; at the same time, develop-mental psychologists can offer connectionism
the fruit of their experience and knowledge of change in real human beings.
Within developmental psycholinguistics, connec-tionism has already resulted
in a reexamination of our assumptions about learnability. There are now
a number of compelling demonstrations of language learning in neural networks,
showing that these systems can (1) extract general principles from finite
and imperfect input, (2) overgeneralize these principles to produce creative
"errors" of the kind that are often observed in children (e.g.,
"comed", "goed", "stooded up"), and (3) recover
from these errors of over-generalization and converge on normal performance
in the absence of negative evidence (for examples, see Plunkett and Marchman,
1991a & b; Marchman, 1992; Elman, 1991a; MacWhinney and Leinbach, 1991).
Some serious criticisms have been raised about the nature and limitations
of neural networks for language learning (Pinker and Prince, 1988; Pinker
and Mehler, l988), but so far each of those criticisms has been countered
effectively (esp. MacWhinney and Leinbach, 1991; Seidenberg, 1992). Besides
the well-known benchmark studies of the English past tense, con-nectionist
simulations of language learning have been carried out in a wide range of
domains. There have been successful demonstrations of language learning
with minimal innate structure in areas of grammar where the traditional
model has had its greatest impact, such as the learning of long-distance
dependencies (a typical example would be the subject-verb agreement relationship
between "BOYS and "ARE" in a sentence like "THE BOYS
that the woman that I saw invited to the party ARE COMING" - Elman,
1991b). Connectionist models have also been applied successfully to problems
that have proven difficult if not intractable for traditional models, fuzzy
categories that defy an explanation in terms of discrete symbols, features
or rules. Examples include "un"-prefixation (e.g., why can we
say "Unhook" but not "Unhug"? - Bowerman, 1982; see
Li, 1992, for a successful simulation of this phenomenon), and German gender
(e.g., why do Germans use a neuter form for "little girl" but
a feminine form for "bottle" - see Maratsos, 1983, for a statement
of the problem, and MacWhinney, Leinbach, Taraban and McDonald, 1989 for
a solution). There have been interesting extensions of this work into simulations
of historical language change (i.e. why do some forms fade away while others
take over across the history of a language? - Hare and Elman, 1992; Thyme,
Ackerman and Elman, 1992), simulations of language processing in the "adult"
net (Elman and Weckerly, 1992), and simulations of language breakdown in
"damaged" nets (Seidenberg and McClelland, 1989; Hinton and Shallice,
1989; Marchman, 1992; Dell and Juliano, 1991; Martin, Saffran, Dell and
Schwarz, 1991). It looks as though this field may be moving toward a unified
theory of how language changes through time, at several different time scales
from milliseconds to centuries. The prospects for productive work on the
nature of language learning are excellent.
Someday someone will no doubt find a set of limitations that these systems
cannot overcome, but at this point in time it is not at all clear what those
limits will be. One reason why we cannot predict the limitations of neural
network models lies in the fact that these models are non-linear dynamic
systems - which brings us to the next point.
(4) Non-linearity in language development
Non-linearity is a fashionable topic in the natural sciences, and it is
a topic that we are beginning to hear more about in research on brain and
behavioral development (Thelen, 1991). We are convinced that non-linearity
will also play a growing role in the next few years in the way we think
about learning and change in the linguistic domain. To make that point,
we need to distinguish between two forms of non-linearity: non-linear outcomes
(i.e. a non-linear relationship between time and behavioral outcomes, which
may be generated by a linear equation) and non-linear dynamics (i.e. change
that is generated by a non-linear equation). These two aspects of non-linearity
have equally important but logically distinct implications for theories
of language development.
By definition, a relationship between two variables is linear if it can
be fit by a formula of the type
y = ax + b
where y and x are variables, and a and b
are constants. Any relationship that cannot be fit by a formula of this
kind is, by definition, non-linear. It is remarkable how much of nature
(including human behavior) can be described by linear equations (at
least within some limited range). And that is a good thing too, because
equations of this kind are very well-behaved, and well understood. Perhaps
for these reasons, behavioral scientists often assume linearity (implicitly
or explicitly) in their efforts to explain patterns of change. We are surprised
when behavioral patterns deviate from linearity on some level, and we are
often tempted to spin complicated stories and postulate external causes
that would not be necessary if we took a non-linear view. Let us illustrate
this point with a few examples.
Figure 2a illustrates a hypothetical linear relation-ship
between two variables, x (on the horizontal axis) and y (on
the vertical axis). For purposes of argument, let us assume that x
refers to a time variable t, and y stands for quantities of
some measurable behavior. In the specific relationship illustration in Figure
2a, t stands for an age range from 6 - 40 years, and y represents
the estimated number of words in the vocabulary of the average English speaker,
from 14,000 words at age 6 (Templin, 1957; see also Carey, 1982) to an estimated
average of 40,000 words at age 40 (McCarthy, 1954)2.
This relationship is a linear outcome, described by the linear equation
y = at + b
where a represents a constant average gain of 730 words per year
(approximately 2 words per day), and b is given a fixed value of
9620 words (necessary to produce the estimated starting value of 14,000
words at age 6). The rate of gain that underlies this relationship can be
described by the following linear dynamic equation (also known as
an evolution equation):
dy/dt = a.
The term dy/dt refers to the range of change in y per unit
of change in t. This dynamic equation can be used to calculate amount
of change in vocabulary on any given application. In contrast with the dynamic
equations that we will consider later, the amount of change per unit time
is constant. That is, we always add 730 words per year, regardless of the
amount of vocabulary that is available before the equation is applied. The
flat line in Figure 2b illustrates this rather uninteresting dynamic relationship.
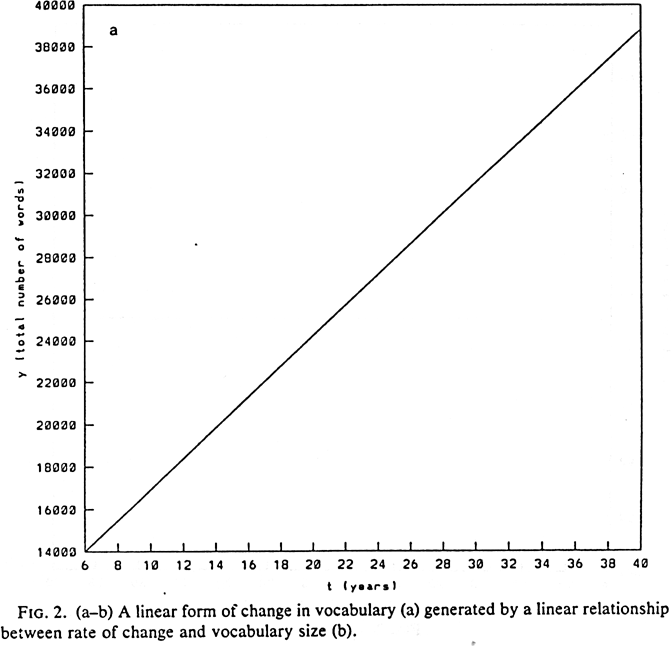
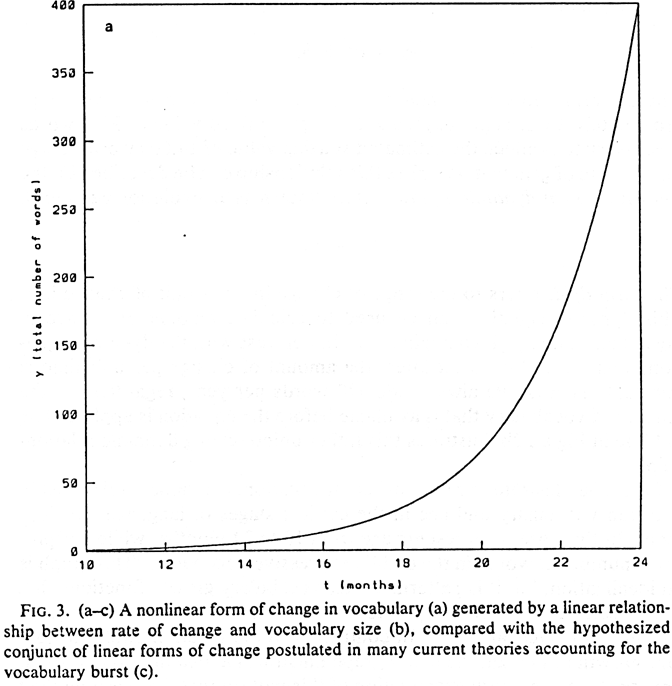
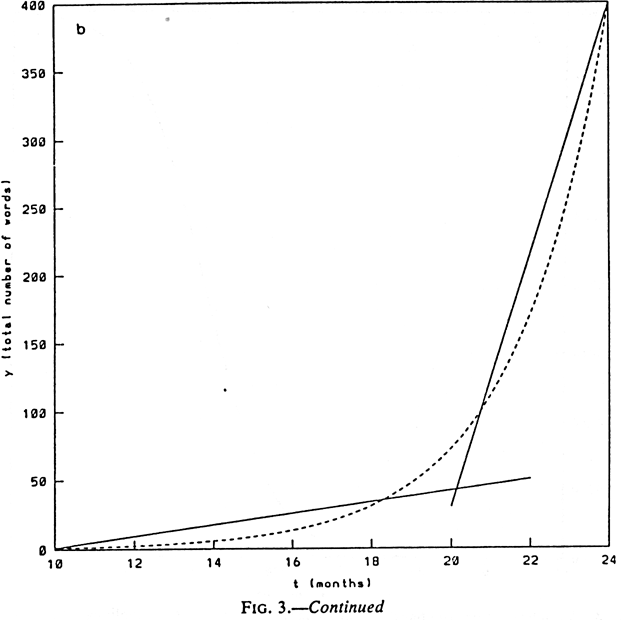
Figure 3a illustrates a rather different situation, a non-linear relationship
between vocabulary and age in the earliest stages of language development.
In this case, t represents age from 10 to 24 months, while y
represents number of words in the child's expressive vocabulary. This graph
is an idealization, but it is patterned after vocabulary growth functions
that have been observed in diary studies of real live human children (e.g.,
Dromi, 1987; Nelson, 1973). In contrast with the graph of adult vocabulary
growth in Figure 2a, the infant graph illustrates a non-linear outcome.
It appears from a cursory examination of this pattern that there is a marked
acceleration somewhere around the 50-word level in the rate at which new
words are added. For example, the child learns only 24 new words between
10 and 14 months, but she learns 328 new words between 20 and 24 months.
This non-linear pattern can be described by the non-linear equation
y = y0 ea(t - t0).
Here y0 =1 is the number of words the child knows at t0 = 10 months of
age (Fenson et al., 1993). The constant a is called the exponential growth
rate (which in this case is 43% per month), and e is the exponential
function. Actually all this function ex means is that the constant e
(which is always approximately 2.718) is raised to the power x. For
example, e2 is the square of e, which is approximately 7.388,
etc.
"Burst" patterns like this one have been reported many times in
the language acquisition literature. They are common in vocabulary development
between 14 and 24 months of age, and similar functions have been reported
for aspects of grammatical development between 20 - 36 months of age. How
should such "bursts" be interpreted? A number of explanations
have been proposed to account for the vocabulary burst. They include "insight"
theories (e.g., the child suddenly realized that things have names - Dore,
1974; Baldwin, 1989), theories based on shifts in knowledge (Zelazo and
Reznick, 1991; Reznick & Goldfield, 1992), categorization (Gopnik and
Meltzoff, 1987), and phonological abilities (Menn, 1971; Plunkett, in press).
Although these theories vary greatly in the causal mechanisms brought to
bear on the problem, they all have one thing in common: The proposed cause
is located at or slightly before the perceived point of acceleration (i.e.
somewhere around 50 words). In a sense, such theories assimilate or reduce
the data in Figure 3a to a pair of linear relationships, illustrated in
Figure 3b, i.e. two linear functions whose cross-point indexes a sudden,
discontinuous change in the "rules" that govern vocabulary growth.
However, if the function illustrated in Figure 3a is accurate, this perceived
point of acceleration is really an illusion. Figure 3a is a smoothly accelerating
function without a single identifiable inflection point, and can be generated
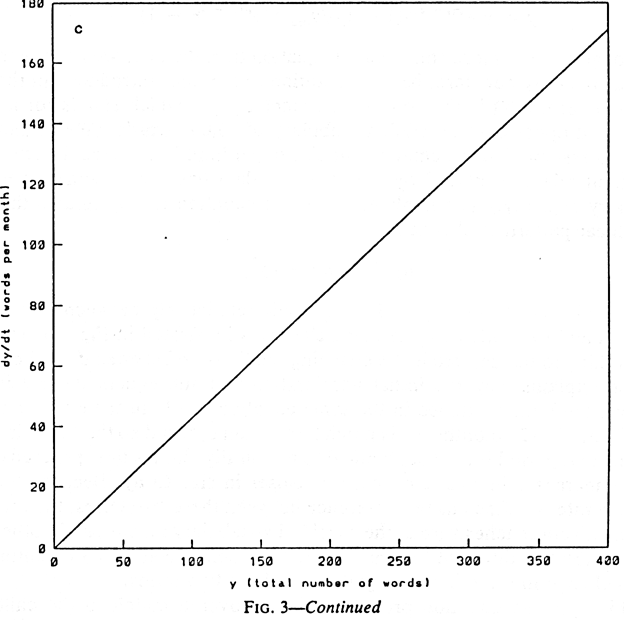
by a linear dynamic equation of the form
dy/dt = ay
which tells us that the increase at any given moment is always proportional
to total vocabulary size. The term a is no longer a constant number
of words (as it was in the previous example), but a constant percentage
per unit time (much like a constant interest rate applied to a growing savings
account). This linear dynamic relationship is illustrated in Figure 3c.
As van Geert (1991) has argued in a recent paper on the equations that govern
developmental functions, we do not need to invoke intervening causes to
explain this kind of growth. The real "cause" of the acceleration
that we commonly observe between 50 - 100 words may be the growth equation
that started the whole process in the first place, i.e. conditions that
have operated from the very beginning of language development. Of course
this does not rule out the possibility that other factors intervene along
the way. Environmental factors may act to increase or reduce the rate of
gain, and endogenous events like the "naming insight" and/or changes
in capacity could alter the shape of learning. Our point is, simply, that
such factors are not necessary to account for non-linear patterns
of change.
On the other hand, there are excellent reasons to believe that the dynamic
equation in Figure 3c tells only part of the story (see also van Geert,
1991). Let us suppose for a moment that vocabulary growth continued to follow
this dynamic function for a few more years. At this rate of growth, our
hypothetical child would have a vocabulary of approximately 68,000 words
at 3 years of age, 12 million words at four years, and 2 billion words by
the time she enters kindergarten! Since there are no known cases of this
sort, we are forced to one of two conclusions: (1) some exogenous force
intervenes to slow vocabulary growth down, or (2) the initial acceleration
and a subsequent deceleration were both prefigured in the original growth
equation. To explore the second option, we need to consider non-linear
outcomes that are brought about by non-linear dynamics.
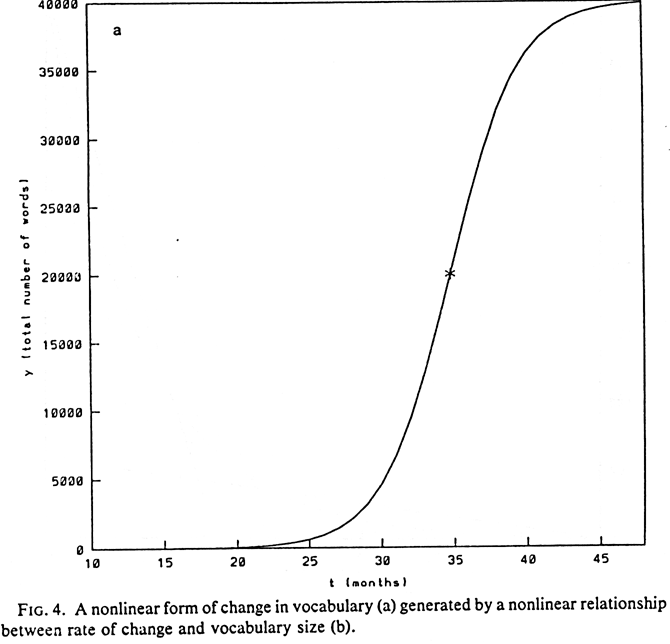
Figure 4a illustrates a relatively simple non-linear pattern known as the
logistic function. Functions of this kind are quite common in behavioral
research, and they are also common in neuroscience (where they can be used
to describe the probability of firing for a single neuron or population
of neurons, assuming some threshold value). The particular example in Figure
4a reflects a hypothetical example of vocabulary growth from approximately
10 to 48 months of age. The first part of the graph from 10 - 24 months
is almost identical to the growth function in Figure 3a (although that is
difficult to see because of the change in scale). In contrast with the ever-increasing
exponential burst in Figure 3a, Figure 4a does have a true "inflection
point" (half-way up the curve), defined as the point at which the rate
of change stops increasing, and starts to slow down. This pattern can be
described by the equation
y = y0 ea(t - t0 ) / (1+ (y0
/ymax (ea(t - t0 ) - 1) ).
Although this is a more complicated equation than the ones we have seen
so far, the only new term here (in addition to the ones introduced in the
previous example) is the constant parameter ymax , which stands for
an estimated upper limit on adult vocabulary of 40,000 words. (We do not
have to assume that the child knows this upper limit in advance; instead,
the limit might be placed by the available data base or by some fixed memory
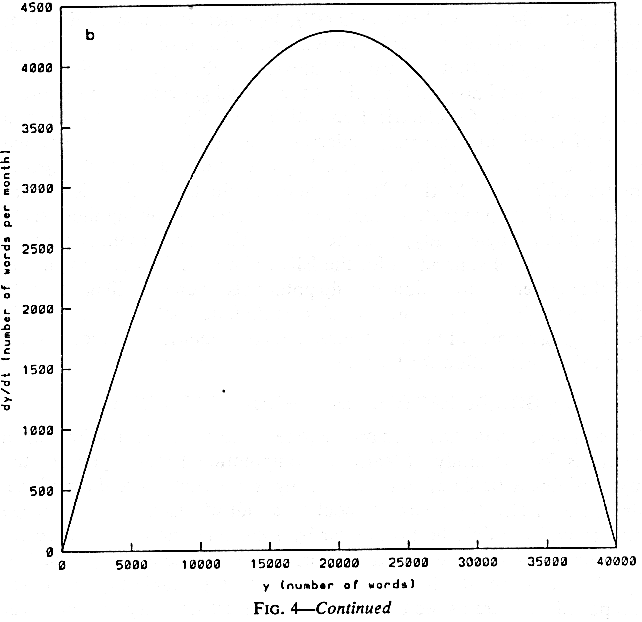
capacity). The non-linear dynamic equation that generates this non-linear
pattern of change is
dy/dt = ay - cy2
where c is defined as a/ymax. This dynamic relationship
between rate of growth and the variable undergoing change is illustrated
in Figure 4b. The main thing to notice here is the changing relationship
between ay and cy2 which explains why the initial acceleration
and subsequent decline in growth are both contained in the same equation.
Early in the evolution, say from 10 to 24 months, ay is much larger
than cy2 and so the evolution during that period is almost identical
to that in Figure 3a. As time proceeds, and y increases in size,
cy2 becomes closer in size to ay. Because the growth rate
is defined as the difference between these two terms, the rate of growth
approaches zero at the specified vocabulary maximum. In other words, the
two different "stages" in development are given by a continuous
change in the relative magnitude of these two terms.
This dynamic equation provides a better overall match to the child vocabulary
growth data than the exponential in Figure 3c (i.e. the function that predicts
a 2 billion-word vocabulary when the child enrolls in kindergarten....).
However, it is still grossly inadequate. In Figure 4a, our hypothetical
child is already close to adult vocabulary levels at 4 years of age - unlikely
under any scenario. In other words, as van Geert also concludes in his analysis
of lexical growth patterns, the symmetrical properties of the logistic function
cannot capture the apparent asymmetries in rate of growth evidenced across
the human life time.
There are two ways out of this dilemma: Abandon our efforts to achieve a
unitary model of growth in this behavioral domain, or adopt a more complex
model. We suspect that we will ultimately have to follow both alternatives.
The particular example of non-linear dynamics illustrated here is only one
of a huge class of possible non-linear dynamic systems. This class includes
an exotic and celebrated form of non-linearity called chaos, famous because
it seems to elude our understanding altogether, being (by definition) completely
deterministic but completely unpredictable. The behavior of non-linear systems
is difficult to predict because they have a property called sensitivity
to initial conditions. In particular, because there is a non-linear
relationship between rate of change and the variable that is undergoing
change, the outcomes that we ultimately observe are not proportional to
the quantities that we start with. A very small difference in the starting
points of two otherwise similar systems can lead (in some cases) to wildly
different results. In principle, all these systems are deterministic; that
is, the outcome could be determined if one knew the equations that govern
growth together with all possible details regarding the input, out to an
extremely large number of decimal places. In practice, it is hard to know
how many decimal places to go out to before we can relax (and in a truly
chaotic system, the universe does not contain enough decimal places). For
this and other reasons, non-linear dynamic systems constitute a new frontier
in the natural sciences. For those of us who are interested in applying
such systems to problems in behavioral development, this is both the good
news and the bad news. The good news is that non-linear dynamic systems
are capable of a vast range of surprising behaviors. The bad news is that
no one really understands how they work or what their limits are.
Whether or not we are comfortable with this state of affairs, it is likely
that the field of child language will be forced to abandon many of the linear
assumptions that underlie current work. We have already shown how linear
assumptions may have distorted our understanding of monotonic phenomena
like the voca-bulary burst. In the same vein, linear assumptions may have
distorted our understanding of non-monotonic phenomena like the famous "U-shaped
curve" in the development of grammatical morphology. Many developmental
psycholinguists have assumed that the sudden appearance of overgeneralization
errors (e.g., from "came" to "comed") reflects the sudden
appear-ance of a new mechanism for language learning and language use, a
rule-based mechanism that is quali-tatively different from the rote and/or
associative mechanism responsible for early learning of irregular verb forms.
The original statement of this argument goes back to Berko (1958); its modern
reincarnation can be found in Pinker (1991 and 1992). It is hopefully clear
by now why this assumption is unwarranted. Discontinuous outcomes can emerge
from continuous change within a single system. Under a continuous increase
in temperature, ice can turn to water and water into steam. By the same
token, continuous learning and/or continuous growth can "bootstrap"
the child into a succession of qualitatively different problems and qualitatively
different behavioral solutions to those problems (for further discussion
of this point, see Bates, Thal and Marchman, 1991).
One of the reasons why connectionist simulations of past-tense learning
have attracted so much attention lies in their ability to produce such discontinuous
outcomes from continuous change, an ability that is based in large measure
on the non-linear properties of multilayered neural nets (Hertz, Krogh and
Palmer, 1991). Like human children, these systems display progress followed
by backsliding, errors that appear and then disappear, change that "takes
off" in unexpected ways that were not predictable from the initial
conditions used to set up the simulation. If it is the case that language
learning in human beings reflects the operation of a non-linear dynamic
system, then we have our work cut out for us. Fortunately, connectionist
models provide some of the tools that we will need to explore this possibility.
(5) Neural correlates of language learning
We are now two years into what Congress has, in its infinite wisdom, declared
to be the Decade of the Brain. Although the implications of this declaration
remain to be seen, it is the case (with or without congressional help) that
we are in the midst of an exciting new era of research on the nature and
development of the human brain. We will not wax too long or eloquent on
this point (for readings on brain development and cognition, see Johnson,
1993), except to stress that some very exciting opportunities await us in
research on the neural correlations of normal and abnormal language development.
First, recent findings in developmental neuro-biology using animal models
have demonstrated far more plasticity in early brain development than we
ever could have imagined (O'Leary, Stanfield and Cowan, 1981; O'Leary and
Cowan, 1984; Merzenich, Nelson, Stryker, Cynader, Schoppman and Zook, 1984;
Merzenich, Recanzone, Jenkins, Allard and Nudo, 1988; Sur, Garraghty,and
Roe, 1988; Sur, Pallas and Roe, 1990; Frost and Schneider, 1979; Frost,
1989). Neuroscientists have literally "re-wired" the developing
brain in various species, demonstrating (for example) the establishment
of somatosensory maps in visual cortex, the establishment of visual maps
in somato-sensory or auditory cortex, and so on. It appears as though the
structuring effects of experience on the brain are far more massive than
previously believed. These findings complement research on normal brain
development by Rakic, Bourgeois, Eckenhoff, Zecevic and Goldman-Rakic (1986);
Huttenlocher (1979); Huttenlocher, de Courten, Garey, and Van der Loos (1982);
Huttenlocher and de Courten, 1987; Changeux (1985); and Changeux and Dehaene
(1989), showing a huge overproduction of neurons (prenatally) and connectivity
(postnatally). These investigators have concluded that the bulk of postnatal
brain development can be characterized by so-called subtractive or regressive
events, the loss of neurons and retraction of connections. Furthermore,
a primary mechanism governing this subtractive process is competition: Connections
that win are maintained and (perhaps) expanded (in second- and third-order
synaptic branching), while connections that lose are eliminated. The basic
message appears to be that experience plays a major role in the creation
of brain structure. Indeed, it has been suggested that experience literally
sculpts and remodels that brain into its adult form. These results may help
to explain the extraordinary plasticity for language development observed
in children with early focal brain injury (Marchman, Miller and Bates, 1991;
Thal, Marchman, Stiles, Aram, Trauner, Nass and Bates, 1991; Aram, 1988;
Riva and Cazzaniga, 1986; Vargha-Khadem, O'Gorman and Watters, 1985). Variations
in this process may also help us to understand milestones and variations
in language development in normal children (Bates, Thal and Janowsky, 1992).
Second, researchers have now begun to apply new techniques for neural imaging
to the study of human brain development, including Magnetic Resonance Imaging
or MRI (Jernigan and Bellugi, 1990; Jernigan, Hesselink, Sowell and Tallal,
1991; Jernigan, Trauner, Hesselink and Tallal, 1991), and Positron Emission
Tomography or PET (Chugani, Phelps and Mazziotta, 1987; Chugani and Phelps,
1991). However, use of these techniques with children will continue to be
limited by ethical constraints (e.g., PET involves injecting a radioactively
tagged substance into children in critical phases of development; MRI is
non-invasive, but often requires use of sedation with very young children).
For this reason, we suspect that many of our greatest insights will come
from less direct but safer techniques for functional brain-imaging through
electrophysiological recording, with particular emphasis on Event-Related
Brain Potentials or ERP - (Molfese, 1990; Mills, Coffey and Neville, 1993
and in press; Kurtzberg, Hilpert, Kreuzer and Vaughn, 1984; Kurtzberg, 1985;
Kurtzberg and Vaughn, 1985; Novak, Kurtzberg, Kreuzer and Vaughn, 1989).
For example, recent studies by Mills, Neville and their colleagues using
this technique have demonstrated systematic changes in brain organization
that are associated with major milestones in language development (e.g.,
the onset of word comprehension, and the later onset of word production).
In addition, they have uncovered some electrophysiological correlates of
individual differences in rate of language learning among normally developing
children (e.g., "early talkers" vs. "late talkers"),
together with some important indices of reorganization in children with
early focal brain injury. Some critics have argued that electrophysiological
techniques are limited in value, because we know so little about the neural
generators in the brain that are responsible for electrical potentials over
the scalp. However, a number of studies are currently underway that combine
the fine-grained temporal resolution of electrical recording over the scalp
with the spatial resolution offered by MRI, PET and another electrophysiological
technique called MEG (magneto-encephalography). By combining these techniques
within a single study, some neuroscientists are convinced that we will find
the neural generators for the ERP. If we can indeed "break the code"
that governs generation of scalp potentials, then we will have a safe and
relatively inexpensive non-invasive technique that can be used in broad-ranging
studies of brain development and cognition, including studies of brain organization
for language.
(6) Social factors in language learning
Our emphasis so far has been on "high technology": new mathematical
formalisms for the study of learning, computational techniques for the analysis
of linguistic data, breakthroughs in structural and functional brain imaging.
Has the heart and soul gone out of research on language learning? Will the
field be taken over by engineers and computer scientists? What hope is there
for the humble behavioral scientist (linguist or psycholinguist) armed with
nothing more than a portable taperecorder and a pencil? We are asked these
questions, in all sincerity (usually over drinks), by child language researchers
who fear that a field low in technology but rich in ideas is about to disappear.
Most child language research relies heavily on traditional observational
and experimental techniques for the study of behavior. And many child language
researchers (including the first author) suffer from some form of math anxiety
and machine phobia. Why, then, should one be optimistic about this Brave
New World? Some friends ask whether we have abandoned com-pletely the study
of language in a social context (cf. Bates, 1976), and others raise the
spectre of "mechanistic thinking" (including one former professor
who startled E.B. with the complaint "You are just as bad as the Chomskians,
with all their gratuitous love of formalism"). Our answer is this:
If one sincerely believes in the social-experiential bases of learning and
change, then there is no reason to fear quantification or precision. Indeed,
the increased precision offered by these new models may make it impossible
to hide from the contributions of social and contextual factors. To illustrate
that point, let us close with our favorite connectionist anecdote.
Two years ago, a colleague of ours who has made great progress in the application
of neural networks to language learning decided to go beyond simulations
using artificial data. He accessed the Child Language Data Exchange System
to obtain transcripts of the language corpora for Roger Brown's famous subject
Adam, and set his neural model to work on the input strings provided by
Adam's mother. Needless to say, this effort failed. But it failed in a very
instructive way. For example, the system crashed entirely (driven into all
kinds of spurious solutions) faced with an input string in which Adam's
mother interrupted her speech to Adam, called out a question to another
adult in the kitchen, and went to answer the phone. As our colleague put
it "Adam knows something that my network does not know!" For one
thing, the network did not know that Mother had just gone to answer the
phone, and that the input string she began before she was interrupted really
"doesn't count".
There is a lot that could be said here about the constraints and biases
that children bring to bear on language learning (Gallistel, 1990), about
"scaffolding" (Rogoff, 1989; Bruner 1985), about the many ways
that parent and child work together to determine the shape and nature of
the input that "counts". This lesson applies not only to the content
of research on language development, but to the research process itself.
In the future, practitioners of high technology and develop-mental researchers
with a wealth of knowledge about real child language will need to "scaffold"
one another, pushing the frontiers of our field forward in ways that neither
could achieve by acting alone. This is the real promise of research on language
development in the next decade.
FOOTNOTES
1 One of us (E.B.)
is the daughter of a weatherman. He met E.B.'s mother shortly after World
War II at the U.S. Weather Bureau office in Wichita, Kansas, where she served
as the "weather girl" for a local radio station. The perils of
forecasting were passed on to their children very early, by angry neighbors
returning from rain-soaked picnics and by beer-soaked uncles passing on
unsolicited vocational advice at holiday gatherings.
2 Word learning is
the simplest system that we could think of to make a succession of points
about the nature of growth. But all of our assumptions are overly simple,
and all of them are based on crude estimates of vocabulary size at any given
point in development. In fact, there are good reasons why better statistics
on child and adult vocabulary are still unavailable. For one thing, there
is no theory-neutral way to calculate vocabulary size. How should we count
inflected forms (e.g., should "dog" and "dogs" each
be listed as separate words)? How about derived forms (e.g., "govern"
vs. "government")? What is the status of compounds (e.g., "watermelon"
and "waterlily" are usually counted as single words, but what
do we do with "water level" or "water nymph")? A serious
treatment of word learning must take problems like these into account. Our
purpose here is not to provide a serious solution, but to introduce a class
of possible solutions to the dynamics of language learning.
REFERENCES
Aram, D. (1988). Language sequelae of unilateral brain lesions in children.
In F. Plum (Ed.), New York: Raven Press. Baker, C.L. (1981). Learnability
and the English auxiliary system. In C.L.
Baker & J.J. McCarthy (Eds.), The logical problem of language acquisition.
Cambridge, MA: MIT Press.
Baldwin, D.A. (1989). Establishing word-object relations: A first step.
Child Development, 60, 381-398.
Bates, E. (1976). Language and context: Studies in the acquisition of pragmatics.
New York: Academic Press.
Bates, E. (1979). The emergence of symbols. New York: Academic Press.
Bates, E., Camaioni, L., & Volterra, V. (1975). The acquisition of performatives
prior to speech. Merrill-Palmer Quarterly, 21, 205-226.
Bates, E., & Elman, J.L. (1993). Connectionism and the study of change.
In M. Johnson (Ed.), Brain development and cognition: A reader. Oxford:
Blackwell Publishers.
Bates, E., Thal, D., & Janowsky, J. (1992). Early language development
and its neural correlates. In I. Rapin and S. Segalowitz (Eds.), Handbook
of neuropsychology, Vol. 7: Child neuropsychology. Amsterdam: Elsevier.
Bates, E, Thal, D., & Marchman, V. (1991). Symbols and syntax: A Darwinian
approach to language development. In N. Krasnegor, D. Rumbaugh, R. Schiefelbusch
and M. Studdert-Kennedy (Eds.), Biological and behavioral determinants of
language development. Hillsdale, NJ: Erlbaum.
Berko, J. (1958). The child's learning of English morphology. Word, 14,
150-177.
Bohannon, N., & Hirsh-Pasek, K. (1984). Do children say as they're told?
A new perspective on motherese. In L. Feagans, K. Garvey & R. Golinkoff
(Eds.), The origins and growth of communication. Norwood, NJ: Ablex.
Bohannon, N., MacWhinney, B., & Snow, C. (1990). No negative evidence
revisited: Beyond learnability or who has to prove what to whom. Developmental
Psychology, 26, 221-226.
Bohannon, N., & Stanowicz, L. (1988). The issue of negative evidence:
Adult responses to children's language errors. Developmental Psychology,
24, 684-689.
Bowerman, M. (1973). Structural relationships in children's utterances:
Syntactic or semantic? In T. Moore (Ed.), Cognitive development and the
acquisition of language. New York: Academic Press.
Bowerman, M. (1982). Reorganizational processes in lexical and syntactic
development. In E. Wanner & L.Gleitman (Eds.), Language acquisition:
The state of the art. New York: Cambridge University Press.
Braine, M. D. S. (1976). Children's first word combinations. Monographs
of the Society for Research in Child Development, 41, (Whole No. 1).
Brown, R. (1973). A first language: The early stages. Cambridge, MA: Harvard
University Press.
Brown, R., & Hanlon, C. (1970). Derivational complexity and order of
acquisition in child speech. In R. Hayes (Ed.), Cognition and the development
of language. New York: Wiley.
Bruner, J.S. (1985). Child's talk - learning to use language. New York:
Norton.
Camaioni, L., Caselli, M.C., Longobardi, E., & Volterra, V. (1991).
A parent report instrument for early language assessment. First Language,
11, 345-359.
Carey, S. (1982). Semantic development: The state of the art. In E. Wanner
& L.Gleitman (Eds.), Language acquisition: The state of the art. New
York: Cambridge University Press.
Changeux, J.P. (1985). Neuronal man. New York: Oxford University Press.
Changeux, J.P., & Dehaene, S. (1989). Neuronal models of cognitive functions.
Cognition, 33, 63-109.
Chugani, H.T., Phelps, M.E., & Mazziotta, J.C. (1987). Positron emission
tomography study of human brain functional development. Annals of Neurology,
22, 487-497.
Chugani, H.T., & Phelps, M.E. (1991). Imaging human development with
positron emission tomography. Journal of Nuclear Medicine, 32, 23-26.
Churchland, P., & Sejnowski, T. (1992). The computational brain. Cambridge,
MA: MIT Press/Bradford Books.
Crain, S. (1992). Language acquisition in the absence of experience. Behavioral
and Brain Sciences, 14, 597-611.
Dale, P.S. (1990). Parent report and the growth of MLU. Unpublished manuscript.
Dale, P. S. (1991). The validity of a parent report measure of vocabulary
and syntax at 24 months. Journal of Speech and Hearing Sciences, 34, 565-571.
Dale, P., Bates, E., Reznick, J. S., & Morisset, C. (1989). The validity
of a parent report instrument of child language at 20 months. Journal of
Child Language, 16, 239-249.
Dell, G.S., & Juliano, C. (1991). Connectionist approaches to the production
of words. Cognitive Science Tech. Rep. CS-91-05 (Learning Series). Urbana,
IL: The Beckman Institute, University of Illinois.
Dore, J. (1974). A pragmatic description of early language development.
Journal of Psycholinguistic Research, 4, 423-430.
Dromi, E. (1987). Early lexical development. Cambridge and New York: Cambridge
University Press.
Elman, J.L. (1991a). Incremental learning, or the importance of starting
small. (Tech. rep. 9101). Center for Research in Language, University of
California, San Diego.
Elman, J.L. (1991b). Distributed representations, simple recurrent networks,
and grammatical structure. Machine Learning, 7, 195-225.
Elman, J.L., & Weckerly, J. (1992). A PDP approach to processing center-embedded
sentences. Manuscript, University of California, San Diego, Center for Research
in Language.
Fenson, L., Dale, P., Reznick, J. S., Thal, D., Bates, E., Hartung, J.,
Pethick S. & Reilly, J., (1993). MacArthur Communicative Development
Invento-ries: User's guide and technical manual. San Diego: Singular Publishing
Group.
Fenson, L., Thal, D., & Bates, E. (1990). Normed values for the "Early
Language Inventory" and three associated parent report forms for language
assessment. Technical report, San Diego State University.
Frost, D. (1989). Transitory neuronal connections in normal development
and disease. In C. Von Euler (Ed.), Brain and reading. London: Macmillan
Press Ltd.
Frost, D.O., & Schneider, G.E. (1979). Plasticity of retinofugal projections
after partial lesions of the retina in newborn Syrian hamsters. Journal
of Comparative Neurology, 185, 1649-1677.
Gallistel, C.R. (1990). The organization of learning. Cambridge, MA: MIT
Press.
Gold, E. (1967). Language identification in the limit. Information and Control,
10, 447-474.
Goldin-Meadow, S., & Mylander, C. (1985). Gestural communication in
deaf children: The effects and non-effects of parental input on early language
development. Monographs of the Society for Research in Child Development,
207.
Goodman, N. (1979). Fact, fiction and forecast. Indianapolis, IN: Hackett.
Gopnik, A., & Meltzoff, A. (1987). The development of categorization
in the second year and its relation to other cognitive and linguistic developments.
Child Development, 58, 1523-1531.
Hare, M., & Elman, J.L. (1992). Connectionist account of English inflectional
morphology: Evidence from language change. Manuscript, University of California,
San Diego, Center for Research in Language.
Hertz, J., Krogh, A., & Palmer, R. (1991). Introduction to the theory
of neural computation. Redwood City, CA: Addison Wesley.
Hinton, G.E., & Shallice, T. (1989). Lesioning a connectionist network:
Investigations of acquired dyslexia. Psychological Review, 98, 74-95.
Huttenlocher, P.R. (1979). Synaptic density in human frontal cortex - developmental
changes and effects of aging. Brain Research, 163,195-205.
Huttenlocher, P.R., de Courten, C., Garey, L.J., & Van der Loos, H.
(1982). Synaptogenesis in human visual cortex: Evidence for synapse elimination
during normal development. Neuroscience Letters, 33, 247-252.
Huttenlocher, P.R., & de Courten, C. (1987). The development of synapses
in striate cortex of man. Human Neurobiology, 6, 1-9.
Hyams, N.M. (1986). Language acquisition and the theory of parameters. Dordrecht:
Reidel.
Jackson-Maldonado, D. (1990, April). Adaptation of parental report language
inventories for Spanish-speaking infants and toddlers. International Conference
on Infancy Studies, Montreal.
Jackson-Maldonado, D., Marchman, V., Thal, D., Bates, E. & Gutierrez-Clellen,
V. (in press). Early lexical acquisition in Spanish-speaking infants and
toddlers. Journal of Child Language.
Jernigan, T., & Bellugi, U. (1990). Anomalous brain morphology on magnetic
resonance images in Williams Syndrome and Down Syndrome. Archives of Neurology,
47, 429-533.
Jernigan, T.L., Hesselink, J.R. Sowell, E., & Tallal, P.A. (1991). Cerebral
structure on magnetic resonance imaging in language- and learning-impaired
children. Archives of Neurology, 48, 539-45.
Jernigan, T.L., Trauner, D.A., Hesselink, J.R. & Tallal, P.A. (1991).
Maturation of human cerebrum observed in vivo during adolescence. Brain,
114, 2037-2049.
Johnson, M. (Ed.) (1993). Brain development and cognition: A reader. Oxford:
Blackwell Publishers.
Jordens, P. (1990). The acquisition of verb placement in Dutch and German.
Linguistics, 28, 1407-1448.
Kurtzberg, D. (1985). Late auditory evoked potentials and speech sound discrimination
by infants. In R. Karrer (Chair), Event-related Potentials of the Brain
and Perceptual/Cognitive Processing of Infants. Symposium presented at the
meeting of the Society for Research in Child Development, Toronto, Canada.
Kurtzberg, D., Hilpert, P., Kreuzer, J., & Vaughn, H. (1984). Differential
maturation of cortical auditory evoked potentials to speech sound in normal
full-term and very low-birth-weight infants. Developmental Medical Child
Neurology, 26, 466-475.
Kurtzberg, D., & Vaughn, H. (1985). Electrophysiologic assessment of
auditory and visual function in the newborn. Clinical Perinatology, 12,
277-299.
Li, P. (1992). Overgeneralization and recovery: Learning the negative prefixes
of English verbs. Manuscript, Center for Research in Language, University
of California at San Diego.
Loeb, D.F., & Leonard, L.B. (1988). Specific language impairment and
parameter theory. Clinical Linguistics and Phonetics, 2, 317-327.
MacWhinney, B. (1991). The CHILDES project: Tools for analyzing talk. Hillsdale,
NJ: Erlbaum.
MacWhinney, B., & Leinbach, J. (1991). Implementations are not conceptualizations:
Revising the verb-learning model. Cognition, 40, 121-157.
MacWhinney, B., Leinbach, J., Taraban, R., & McDonald, J. (1989). Language
learning: Cues or rules? Journal of Memory and Language, 28, 255-277.
MacWhinney, B., & Snow, C. (1985). The child language data exchange
system. Journal of Child Language, 12, 271-296.
Maratsos, M. (1983). Some current issues in the study of the acquisition
of grammar. In J. Flavell & E. Markman (Eds.), Handbook of Child Psychology
(Vol. 3). New York: Wiley.
Marchman, V. (1992). Language learning in children and neural networks:
Plasticity, capacity, and the critical period. (Tech. rep. 9201). Center
for Research in Language, University of California, San Diego.
Marchman V., Miller, R., & Bates, E. (1991). Babble and first words
in children with focal brain injury. Applied Psycholinguistics, 12, 1-22.
Martin, N., Saffran, E.M., Dell, G.S., & Schwartz, M.F. (1991, October).
On the origin of paraphasic errors in deep dysphasia: Simulating error patterns
in deep dyslexia. Paper presented at the Deep Dyslexia meeting, London.
McCarthy, D. (1954). Language development in children. In L. Carmichael
(Ed.), Manual of Child Psychology. (2nd ed., pp.492-630). New York: John
Wiley & Sons.
Menn, L. (1971). Phonotactic rules in beginning speech. Lingua, 26, 225-251.
Merzenich, M.M., Nelson, R.J., Stryker, M.P., Cynader, M.S. Schoppman, A.,
& Zook, J.M. (1984). Somatosensory cortical map changes following digit
amputation in adult monkeys. Journal of Comparative Neurology, 224, 591-605.
Merzenich, M.M., Recanzone, G., Jenkins, W.M., Allard, T.T., & Nudo,
R.J. (1988). Cortical representational plasticity. In P. Rakic & W.
Singer (Eds.), Neurobiology of neocortex. (pp. 41-67). New York: John Wiley
& Sons.
Molfese, D. (1990). Auditory evoked responses recorded from 16-month-old
human infants to words they did and did not know. Brain and Language, 38,
596-614.
Mills, D., Coffey, S., & Neville, H. (in press). Language acquisition
and cerebral specialization in 20-month-old children. Journal of Cognitive
Neuroscience.
Mills, D., Coffey, S., & Neville, H. (1993). Changes in cerebral organization
in infancy during primary language acquisition. In G. Dawson and K. Fischer
(Eds.), Human behavior and the developing brain. New York: Guilford Publications.
Nelson, K. (1973). Structure and strategy in learning to talk. Monographs
of the Society for Research in Child Development, 38, (1-2, Serial No. 149).
Novak, G., Kurtzberg, D., Kreuzer, J., & Vaughn, H. (1989). Cortical
responses to speech sounds and their formants in normal infants: Maturational
sequence and spatiotemporal analysis. Electro-encephalography and Clinical
Neurophysiology, 73, 295-305.
O'Grady, W., Peters, A.M., & Masterson, D. (1989). The transition from
optional to required subjects. Journal of Child Language, 16, 513-529.
Ogura, T. (1991). Japanese version of MacArthur CDI. Paper presented at
the 32nd Congress of the Japanese Educational Psychological Association
and at the 2nd Congress of the Japanese Developmental Psychological Association.
O'Leary, D.M., Stanfield, B.B., and Cowan, W.M. (1981). Evidence that the
early postnatal restriction of the cells of origin of the callosal projection
is due to the elimination of axonal collaterals rather than to the death
of neurons. Developmental Brain Research, 1, 607-617.
O'Leary, D.M., & Cowan, W.M. (1984). Survival of isthmo-optic neurons
after early removal of one eye. Developmental Brain Research, 12, 293-310.
Piatelli-Palmarini, M. (1989). Evolution, selection and cognition: From
"learning" to parameter setting in biology and the study of language.
Cognition, 31:1, 1-44.
Pinker, S. (1979). Formal models of language learning. Cognition, 7, 217-283.
Pinker, S. (1981). On the acquisition of grammatical morphemes. Journal
of Child Language, 8, 477-484.
Pinker, S. (1984). Language learnability and language development. Cambridge,
MA: Harvard University Press.
Pinker, S. (1991). Rules of language. Science, 253, 530-535.
Pinker, S. (1992, April). The psychological reality of grammatical rules:
Linguistic, historical, chronometric, psychophysical, computational, developmental,
neurological, and genetic evidence. Paper presented at the 21st Annual Linguistics
Symposium, University of Wisconsin, Milwaukee.
Pinker, S., & Mehler, J. (1988). Connections and symbols. Cambridge,
MA: MIT Press.
Pinker, S., & Prince, A. (1988). On language and connectionism: Analysis
of a parallel distributed processing model of language acquisition. Cognition,
28, 73-193. Pizzuto, E., & Caselli, M.C. (in press). Acquisition of
Italian morphology and its implications for models of language development.
Journal of Child Language.
Plunkett, K. (in press). Lexical segmentation and vocabulary growth in early
language acquisition. Journal of Child Language.
Plunkett, K., & Marchman, V. (1991a). U-shaped learning and frequency
effects in a multi-layered perceptron: Implications for child language acquisition.
Cognition, 38, 43-102.
Plunkett, K., & Marchman, V. (1991b). From rote learning to system building.
In D.S. Touretzky, J. Elman, T. Sejnowski and G. Hinton (Eds.), Connectionist
models: Proceedings of the 1990 Summer School. San Mateo, CA; Morgan Kaufman,
201-219.
Radford, A. (1990). Syntactic theory and the acquisition of English syntax.
Oxford: Basil Blackwell. Rakic, P., Bourgeois, J.P., Eckenhoff, M.F., Zecevic,
N., & Goldman-Rakic, P.S. (1986). Concurrent overproduction of synapses
in diverse regions of the primate cerebral cortex. Science, 232, 232-235.
Riva, D., & Cazzaniga, L. (1986). Late effects of unilateral brain lesions
before and after the first year of life. Neuropsychologia, 24, 423-428.
Reilly, J. (1992). American Sign Language version of MacArthur CDI. Manuscript,
San Diego State University.
Reznick, J. S. & Goldfield, B.A. (1992). Rapid change in lexical development
in comprehension and production. Developmental Psychology., 28, 406-413.
Reznick, J. S., & Goldsmith, S. (1989). Assessing early language: A
multiple form word production checklist. Journal of Child Language, 16,
91-100.
Roeper, T., & Williams, E. (Eds.). (1987). Parameter setting. Dordrecht:
Reidel.
Rogoff, B. (1989). Apprenticeship in thinking: Cognitive development in
social context. New York: Oxford University Press.
Rumelhart D., & McClelland J.L., (Eds.)..(1986). Parallel distributed
processing: Explorations in the microstructure of cognition. Cambridge,
MA: MIT Press.
Seidenberg, M.S. (1992). Connectionism without tears. In S. Davis (Ed.),
Connectionism: Theory and practice. Oxford: Oxford University Press.
Seidenberg, M., & McClelland, J. (1989). A distributed developmental
model of word recognition and naming. Psychological Review, 96, 523-568.
Shore, C. (1986). Combinatorial play: Conceptual development and early multiword
speech. Developmental Psychology, 22, 184-190.
Shore, C., O'Connell, C., & Bates, E. (1984). First sentences in language
and symbolic play. Developmental Psychology, 20, 872-880.
Sokolov, J., & MacWhinney, B. (1990). The CHIP framework: Automatic
coding and analysis of parent-child conversational interaction. Behavioral
Research Methods, Instruments, and Computers, 22, 151-161.
Sokolov, J., & Snow, C.E. (1992, April). Some theoretical implications
for individual differences in the presence of implicit negative evidence.
Paper presented at the 21st Annual Linguistics Symposium, University of
Wisconsin, Milwaukee.
Sur, M., Garraghty, P.E., & Roe, A.W. (1988). Experimentally induced
visual projections into auditory thalamus and cortex. Science, 242, 1437-1441.
Sur, M., Pallas, S.L., and Roe, A.W. (1990). Cross-modal plasticity in cortical
development: Different-iation and specification of sensory neocortex. TINS,
13, 227-233.
Templin, M.C. (1957). Certain language skills in children - their development
and inter-relationships. Minneapolis, MN: University of Minnesota Press.
Thal, D., & Bates, E. (1988). Language and gesture in late talkers.
Journal of Speech and Hearing Research, 31, 115-123.
Thal, D., Marchman, V., Stiles, J., Aram, D., Trauner, D., Nass, R., &
Bates, E. (1991). Early lexical development in children with focal brain
injury. Brain and Language, 40, 491-527.
Thal, D., Tobias, S., & Morrison, D. (1991). Language and gesture in
late talkers: A one-year follow-up. Journal of Speech and Hearing Research,
34:3, 604-612.
Thelen, E. (1991). Improvisations on the behavioral-genetics theme. Behavioral
and Brain Sciences, 14, 409-409.
Thyme, A., Ackerman, F., & Elman, J.S. (1992, April). Finnish nominal
inflection: Paradigmatic patterns and token analogy. Paper presented at
the 21st Annual UWM Linguistics Symposium on The Reality of Linguistic Rules,
Milwaukee.
Valian, V. (1990). Null subjects: A problem for parameter-setting models
of language acquisition. Cognition, 35, 105-122.
Valian, V. (1991). Syntactic subjects in the early speech of American and
Italian children. Cognition, 40, 28-81.
van Geert, P. (1991). A dynamic systems model of cognitive and language
growth. Psychological Review, 98, 3-53.
Vargha-Khadem, F., O'Gorman, A., & Watters, G. (1985). Aphasia and handedness
in relation to hemispheric side, age at injury and severity of cerebral
lesion during childhood. Brain, 108, 677-696.
Wexler, K., & Culicover, P.W. (1980). Formal principles of language
acquisition. Cambridge, MA: MIT Press.
Zelazo, P.D., & Reznick, J. S. (1991). Age-related asynchrony of knowledge
and action. Child Development, 62, 719-735.








