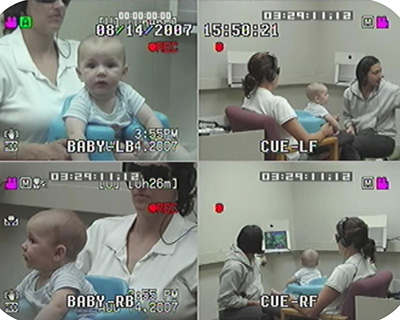
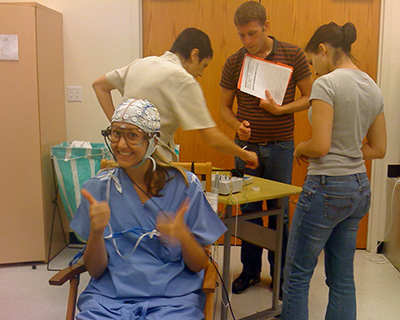
CRL brings together faculty, students and research associates who share an interest in the nature of language, the processes by which language is acquired and used, and the mediation of language in the human brain.
CRL is housed in the Cognitive Science Building on the Thurgood Marshall Campus at the University of California, San Diego and boasts an interdisciplinary academic staff comprised of specialists in a wide variety of fields:
- Cognitive science
- Communication
- Communication disorders
- Computer science
- Developmental psychology
- Linguistics
- Neurosciences
- Pediatrics
- Psycholinguistics
Social Media
CRL Newsletter
CRL is excited to present the latest CRL Newsletter, featuring technical report:
Language Skills and Speed of Auditory Processing in Young Children
J.A. Avenzino, M. Gonzalez Robledo, & G.O. Deák
So-One Hwang, CRL postdoc, won the Mouton de Gruyter Prize for Best Early Career Presentation for her talk "Temporal Integration Windows in Sign Language Processing". Her co-authors on the presentation were Clifton Langdon, Concetta Pucci, William Idsardi & Gaurav Mathur.
Doctoral student Ryan Lepic won the Sign Language Linguistics Society (SLLS) Best Student Poster Award for his poster "Motivation in two-handed signs: A cross linguistic investigation of word form" in collaboration with Gal Belsitzman, Carl Borstell & Wendy Sandler.
Doctoral student Jonathan Udoff won the SLLS Best Student Presentation Award for "Mouthings and their Reductions: A Kinematic Approach" in collaboration with Ignatius Nip.