CRL Newsletter

Vol. 10, No. 1

October 1995

Technical Report

Representing the Structure of a Simple Context-Free Language in a Recurrent Neural Network: A Dynamical Systems Approach

Paul Rodriguez

Department of Cognitive Science, UCSD

ABSTRACT

Parallel Distributed Processing (PDP) architectures demonstrate a potentially radical alternative to the traditional theories of language processing that are based on serial computational models.  However, learning complex structural relationships in temporal data presents a serious challenge to PDP systems. For example, automata theory dictates that processing strings from a simple Context-Free Language(CFL) requires a memory device. This project will employ standard backpropagation training techniques for a Recurrent Neural Network (RNN) in the task of learning a simple CFL.

I will show that a RNN can learn to recognize the structure of a simple CFL; and using Dynamical Systems Theory, one can correctly identify how network states reflect that structure. An important question that arises is whether or not the RNN performs similarly or not to discrete automata.

1. INTRODUCTION

It is well established that sentences of natural language are more than just a linear arrangement of words. Sentences have complex temporal structures that are often characterized syntactically, such as phrase structures, subject-verb agreement, and relative-clauses. Representing and processing such structure presents a critical challenge to mechanisms of natural language processing (NLP), both as a gauge of their theoretic capability and their potential to provide a pyschological account of natural language parsing. Ideally, a mechanism should reflect the nature of the process as well as how it is implemented.

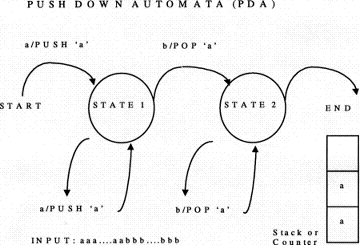
A traditional view of NLP is based on mechanisms of discrete finite automata. Automata theory states that a regular language can be processed by a Finite State Machine (FSM). However, if a language has center-embedding, then that language is a Context-Free Language(CFL) which requires a Push-Down Automata(PDA). Importantly, a PDA is a FSM with an additional resource of a memory-like device that is a "stack" or "counter" in order to keep track of the embeddings (figure 1).

Parallel Distributed Processing (PDP) architectures demonstrate a potentially radical alternative to the traditional theories of language processing. However, learning complex structural relationships in temporal data presents a serious challenge to PDP systems. Here I show that a Recurrent Neural Network (RNN) can learn a simple CFL. Furthermore, I use Dynamical Systems Theory to demonstrate how the RNN reflects the functional requirements of a CFL. In particular, the net can organize resources in order to keep track of input and maintain informational states that reflect the temporal structure of the input. The analysis enables a rough comparison to PDA. This work is complementary to theoretic analysis of RNN capabilities (e.g. Siegelmann) yet original in its specific identification of dynamic properties involved. The work is distinct to other proposed modelling of CFL, such as sequential recursive auto-associative memory (RAAM, e.g. Kwasny and Kalman, 1995), in that I am not directly attempting to represent constituent structures. An important question that arises is: How does a RNN compare to a PDA?

2. RECURRENT NEURAL NETWORKS

2.1 Description

Neural network architectures demonstrate a potentially radical alternative to the traditional discrete automata. A neural network system has no explicit state definitions nor explicit memory stores, but rather consist of simple neuron-like nodes (or units) which are linked together via weighted-connections so that the activation value of a node is a function of weights and activation values from nodes that are directly connected to it. Weights can be adjusted through an error correction procedure (backpropagation) which allows the network to learn input-output mappings (Rumelhart, Hinton, and Williams, 1986).

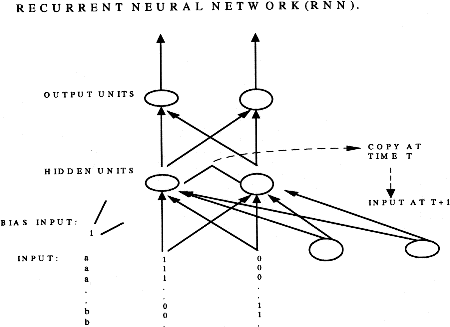
A recurrent neural network (RNN) architecture contains feedback connections which allow the system to have node activation values at one time step affect the same node activation values at the next time step, thereby reflecting temporal processing. Figure 2 presents a typical RNN architecture with two binary-valued input nodes,(shown as input lines), two hidden nodes, two output nodes, and one bias node. The feedback connections are implemented through copy units and the weights can also be updated through appropriate error correction procedures (Elman, 1991; St. John, 1992).

2.2 RNN and Language

Empirical investigations using RNNs with simple artificial grammars have shown that a RNN can learn to recognize strings from a RG (Giles et al., 1992; Giles et al., 1993; Waltrous and Kuhn, 1992; Servan-Shrieber, et al., 1989; Smith and Zipser, 1989). However, relatively little conclusive work has been done using RNNs with artificial CFGs, nor has it been shown how a RNN might perform the same functions as a PDA in processing strings from a CFG. A sequential version of the RAAM model was shown to have compositional structure yet it was not shown how it might generalize on long input strings (Kwasny and Kalman, 1995). Recently, it was shown that a RNN can perform recognition of strings from a CFG, but the network could not generalize properly (Batali, 1994).

Empirical investigations using natural language input have not demonstrated conclusive results on sentence processing capabilities of RNNs.1 For example, Elman reports a RNN that can learn up to three levels of center-embeddings (Elman, 1991). Stolke reports a RNN that can learn up to two levels of center-embeddings, and up to five levels for tail-recursion (Stolke, 1990). Other work has shown that a RNN can process temporal semantic cues within sentences and reflect semantic constraints and associations (St. John, 1990).

Interestingly, it has been shown that a RNN can handle more levels of embedding if there are additional semantic constraints (Weckerley and Elman, 1992). The authors suggest that the RNN is a mechanism that reflects performance. However, in all these latter studies it may be the case that the RNN is performing the functional equivalent of a FSM. In other words the RNN may not appropriately reflect syntactic structure of complex sentences as does a PDA. Perhaps RNN capabilities are inherently limited such that performance is only reflected gratuitously. The current state of affairs presents a dilemma for RNN enthusiasts - they have a mechanism that reflects some aspects of performance, but they do not yet have a theory about the "nature of the solution".

3. THE EXPERIMENT

3.1 Issues

The broader question that situates my research is the issue of how a RNN may suggest an alternative psychological description of syntactic processing tasks. However, I will not directly address this question. Rather I will be addressing two related questions that work toward the bigger issue:

• Can a RNN learn to process a simple CFL?
• What are the states and resources employed by the RNN?

The first question demands that a RNN learn to process a simple CFL so that it generalizes beyond those input/output mappings presented in training. In other words, the performance of the RNN must somehow reflect the structure of the input. The second question demands a functional description of how the RNN reflects the structure of the input. Ideally, one should ground the functional description of states and resources on a formal analysis of the RNN dynamics. Next I will describe the RNN experiment and later I will introduce concepts from Dynamical Systems Theory as the method of analysis.

3.2 RNN Experiment

The input stimuli is a very simple CFL that uses only two symbols, {a, b}, and consists of strings of the form a^n b^n, in which "n" is an integer greater than 0. The training set consists of all strings of total length up to 22, or n=11, which means 11 a's followed by 11 b's. There are more proportionately more short strings than long strings in a ratio of 10 to 1 of shortest to longest. A network that properly generalizes will correctly process strings beyond length n=11.

The architecture for the experiment will be a RNN with 2 input units, 2 hidden units, 2 copy units, 2 output units, 1 bias unit (see figure 2). In one time step the hidden unit activation values and then output unit activation values will be updated. The copy units will hold the hidden unit values in preparation for the next time step.

The RNN will be trained to predict the next input such that if a network makes all the right predictions possible then the network is correctly processing the input. Elman points out several advantages in the prediction task; for one it requires minimal commitment to defining the role of an external teacher, and more importantly it is psychologically motivated by the observation that humans use prediction and anticipation in language processing (Elman, 1991).

For the simple CFL input a^n b^n, when the network has "a" input, it will not be able to accurately predict the next symbol because the next symbol can be another "a" or the first "b" in the sequence. On the other hand, when the network has a "b" input, it could accurately predict the number of "b" symbols that match the number of "a" input, and then also predict the end of the string (Batali, 1994). Correct processing of a string is defined as follows:

• A) "b" input => predict only "b" symbols, except for B).
• B) last "b" input => predict end of the string (or beginning of the next string).

(Since the network outputs values are continuous, I will use a cut off value at .5.)

3.3 Overall Results

I will present two cases of the RNN training results. Both cases use the same network architecture and training set, different sets of initial weights, and were trained to the point of best performance. The first network learned proper predictions for n=8 and the second learned proper predictions for n=16, for a total string length of 32. I claim that the first case attempts to solve the problem in an intuitive way, although it fails. The second case found a solution that does generalize, although the solution will be non-intuitive and will require a dynamical systems analysis. Consequently, before I present the results in detail, in the next section I will introduce the concepts and formalisms of dynamical systems theory.

4. METHOD OF ANALYSIS

4.1 Dynamical Systems Theory as Method

How does one compare and contrast a RNN to finite automata, such as FSM or PDA? The difficulty of the question stems from the fact that a RNN contains node activations that consist of a real number between 0 and 1, whose value is a function of previous node activations and current inputs. In fact, the set of values represent a coordinate point in a high-dimensional vector space defined over real numbers, which implies that two sets of node values have some meaningful measure of distance. On the other hand, in finite automata, such as a FSM or PDA, there exists a predefined set of discrete states and a transition functions which maps current states and current input into a next state. The states have no topological meaning and there is no middle ground between them. Recent work has formally compared a RNN to a FSM by analyzing the RNN performance using mathematical techniques from dynamical systems theory (Casey, 1995; also Tino, Horne, and Giles, 1995). In a similar vein, I will use dynamical systems theory techniques to evaluate a RNN and draw comparisons to PDA.

4.2 Dynamical Systems Overview

A dynamical system is often used to describe real physical systems in which the state of the system at some time depends on the state at a previous time. Many concepts can be introduced by describing some simple physical systems. For example consider a ball placed on a 3-D landscape (figure 3). Depending on where the ball is initially placed, the ball will roll around to some lowest point that it can reach. The position of the ball at some time depends on the position of the ball at some previous time. If the ball is at rest then it is at a "fixed point". If the fixed point is at the bottom of a valley then it is called an attracting fixed point. If the fixed point is at the top of a hill then it is called a repelling fixed point because with a slight perturbation the ball will roll away. The path that the ball takes is called a trajectory.

The 3-D physical landscape can be characterized by a vector flow field in a phase space diagram. The vector flow field represents the set of possible trajectories and the phase space diagram coordinate axis that represent the state variables of the system.2 In this example the state variables are the {x, y} coordinate point of the ball position. For each position on the landscape, the vector flows describe the change of position. In fact, the entire trajectory of the ball can be roughly plotted out in the phase space diagram.

4.3 A RNN is a Dynamical System

A RNN is a system that can be characterized as a discrete-time dynamical system. Since the weight parameters are held constant after training, if the input values are held constant for several time steps, then the hidden unit activation values are the state variables in a phase space diagram. The coordinate system of the phase space diagram would be the pair {hidden unit 1, hidden unit 2} and the vector flow field would give a qualitative description of the change in activation values over several time steps (i.e. a trajectory). Note that for each input there will be a different set of dynamics. Hence for my experiment, there will be one phase space diagram for "a" input, and one diagram for "b" input.

Since the output units are a function of the hidden unit values it will be informative to draw a contour plot on the phase space diagram for each output unit. I will draw a one-line contour plot which cuts up the phase space such that for all {hidden unit 1,hidden unit 2} values on one side of the line the output unit is > .5 or .5 (threshold value).

4.4 Dynamical Systems Analysis

For a discrete-time dynamical system one can use a standard technique ("linearization") for analyzing the behavior near a fixed point. The technique produces a linear system for which the eigenvalues3 govern how the trajectories are contracting or expanding. The eigenvalues give the rate of contraction or expansion and the eigenvectors give the axis along which the system contracts or expands. For example:

• a) eigenvalues > 1 or -1 => system is expanding and the fixed point is repelling,
• b) eigenvalues 1 and > -1 =>system is contracting and the fixed point is attracting,
• c) at least one eigenvalue > 1 or -1 => system is expanding in the direction of the eigenvector that corresponds to that eigenvalue and the fixed point is also a repelling point specifically referred to as a saddle point.

5. RESULTS

I will present two cases of the RNN training results. Case 1 learned the training set only for n=8; case 2 learned the training set completely and generalized for n=16. I will present first a graphical analysis of network performance using vector flow fields and graphing the trajectories (all diagrams are attached at the end). The graphical analysis will only provide a qualitative description of the network dynamics and provide some insights into the mathematical analysis that follows later.

5.1 Case 1

The output units cut up the phase space evenly along a nearly vertical line, such that all {HU1, HU2} (where HU is abbreviation for hidden unit) values to the left of the line predict an "a", and all {HU1,HU2} values to the right predict a "b". Most networks independent of overall performance divided the phase space evenly, although not necessarily vertically. This will be shown on trajectory diagrams below as a line in diagram.

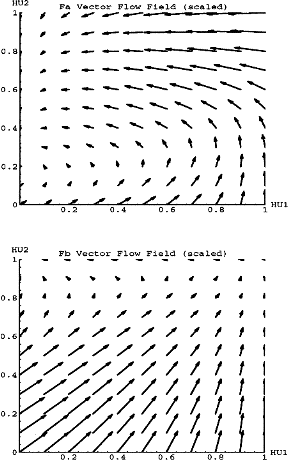
Figure 4 shows the vector flow field for the two input conditions. Note that the vectors are scaled from their true magnitude, but the relative vector size still reflects relative change in {HU1, HU2}. " Fa" and "Fb" represent the dynamics for the "a" input condition and "b" input condition respectively. Note that Fa has an attracting point near (0,.35), and Fb has an attracting point near (0,1). In the physical metaphor the Fa landscape has a valley that slopes down to (0,.35), and Fb has a valley that slopes down to (0,1). One can imagine placing a ball on the Fa hill, letting it roll for a while, and then holding the ball steady at some location while the landscape is instantaneously switched to Fb. Now the ball will change directions and roll around to the other attracting point. This is exactly analogous to feeding the network some strings of the form "aa...aabb...bb".

The landscape analogy has at least one caveat. In real landscapes a ball will roll quickly down from a hilltop and perhaps roll past a small valley, depending on speed, momentum, etc.. However, in the RNN dynamics there is an important rule of thumb: the trajectory will always have small changes near a fixed point - for both attracting and repelling points.

Figure 5 shows the trajectory for some short strings, n=2 and n=3. Each arrow represents 1 time step, hence 1 input. The tail of the arrow is the value of {HU1, HU2} before the time step (i.e. the copy units) and the head represents the updated value of {HU1, HU2} after applying the activation functions. Note that the initial value was chosen by allowing the network to run for one or two short strings. Importantly, the last "b" input results in a change in {HU1, HU2} that crosses over to the left of the dividing line, hence the network properly predicts an "a" when the last "b" is input. Not surprisingly the last {HU1, HU2} value is near the initial starting value.

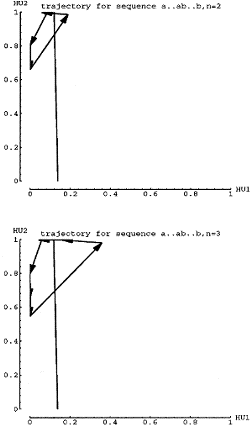
Figure 6 shows the trajectories for longer strings: n=4 and n=5. As above, the network trajectory correctly crosses the dividing line on the last "b" input. Figure 7 shows the trajectories for n=8 and n=9. Note how the network arrows are increasingly shorter near the Fa attracting fixed point. Also, the first "b" input cause a transition to a region of phase space where the arrows can take smaller step sizes as well. However, for n=9 the network crosses the dividing line on the 8th "b", suggesting that perhaps the step sizes are not properly matched.

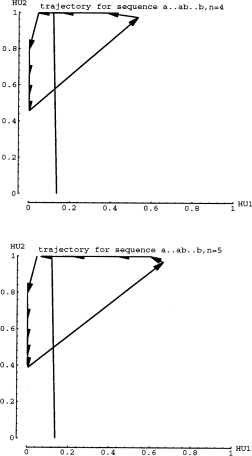
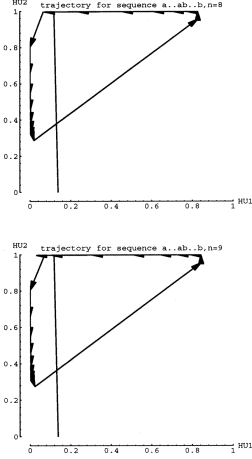
One important feature is that the case 1 network performed most of the processing of "a" input along the HU2 axis, and most of the processing for "b" input along the HU1 axis. In fact, Fa monotonically decreased in HU2, and Fb monotonically decreased in HU1, which intuitively suggests that the network is "counting a's" and then "counting b's", with a transition from "a" to "b" that attempts to set up a proper "b" starting point.

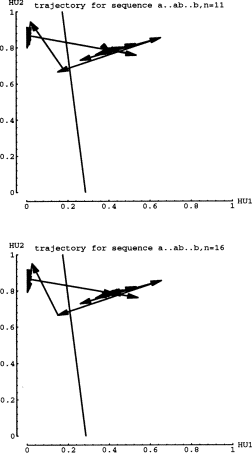
5.2 Case 2

The case 2 network also has output values that divide the phase space along a nearly vertical line (but not all networks have vertical dividing lines). The flow fields in figure 8 show that Fa has an attracting point near (0,.85). The Fb also seems to have an attracting point near (.4,.8), however, the dynamics for Fb turn out to be more complicated. In fact, with simple computer iteration of the network activation functions it was determined that Fb will eventually settle into a periodic-2 fixed point. Therefore in figure 9 I show the dynamics for Fb and for Fb^2, (the composite of Fb with itself). One can now see that Fb^2 has 2 fixed points, near (0,.4) and (1,1). Since, a fixed point for Fb^2 is a periodic point for Fb, we can see that the Fb vector flow field shows not an attracting point but actually a repelling point. The trajectories will show that the network oscillates around the repelling point and eventually settles into the periodic 2 fixed point. The oscillations are the reason that the vectors point toward the repelling point in the Fb dynamics in figure 8. The landscape metaphor would be a large hill with a valley below it, but the valley has a smaller hill in the middle of it such that a ball will roll down the hill towards the small hill but then roll towards the lower points in the valley.

Figure 10 shows the trajectories for short strings, n=2 and n=3. Again the arrows represent 1 time step, hence 1 input. In the next figure, n=4 and n=5, one can see that the trajectories are actually oscillating around both the attracting point and the repelling point. Figure 12 confirms that the oscillations are somehow matched up for longer strings. In other words, if the last "a" input ends up a little higher(or lower) than the attracting fixed point, then the "b" input must transition to a coordinate point that is also higher (or lower) than the repelling fixed point. Also, the smaller arrows of Fa must be matched by small arrow of Fb. As the Fb trajectory steps expand around the repelling point, the network will cross the dividing line on the last expanding step after taking the correct number of total smaller steps. I will refer to such complementary dynamics as coordinated trajectories.

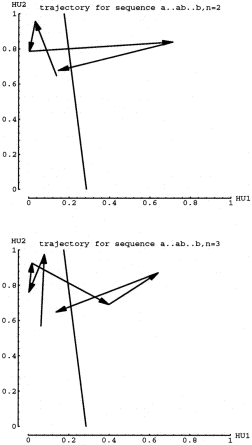
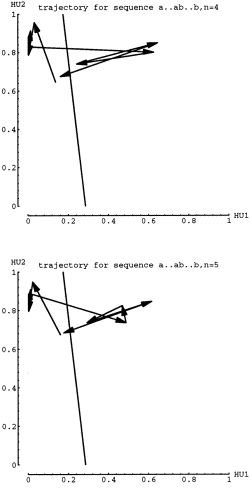
5.3 Analysis Results

In this section I will develop a deeper analysis of the networks and establish some informal criteria that explain how a network is successful. The analysis employs a standard technique of 'linearization' around the fixed point for each input condition. I will be using this technique to compare the trajectory for Fa and Fb. Since the graphs show that the interesting dynamics occur in the neighborhoods around the attracting point for Fa and the saddle point for Fb, I will use these two points as the fixed points in the linearization method.4 In the physical metaphor these points correspond to a valley in the Fa landscape, and a hilltop in the Fb landscape.

The results in table 1 summarize my findings. I have added two other cases of networks with the same architecture trained on the same task, although with different combinations of initial seed, training set, and eta values. Case 3 is a network that had dynamics similar to case 1.5 Case 4 is a network with dynamics similar to my case 2, which was found by Janet Wiles in related work.

             CASE     max n learned      Fa       Fb      1/Fa
             ----     -------------   ------   --------  --------
               1           8           .408      .832     2.45
               2          16          -.7095   -1.455*   -1.409*
               3           7           .242     1.29      4.136
               4          25          -.637    -1.536**  -1.57**

Table 1. A comparison of largest eigenvalues at the attracting fixed point of Fa and repelling fixed point of Fb. The successful networks have eigenvalues that are inversely proportional to each other. The starred values indicate which values are proportional.

The table compares the largest eigenvalues of the Fa system with the largest eigenvalue of the Fb system. These eigenvalues are associated with the eigenvectors that correspond to the axis of contraction under Fa, and the axis of expansion Fb.6 The contraction and expansion rates, which are given by the eigenvalues, indicate the change in hidden units values from one time step to the next. In other words, the size of the trajectory step, as seen in the graphical analysis, is completely determined by the eigenvalues. If the eigenvalues are inversely proportional, then step sizes for "a" input will be matched by step sizes for "b" input. In the landscape metaphor, if the eigenvalues of Fa and Fb are exactly proportional to each other, then the upward slope of the valley in the Fa landscape matches the downward slope of the hilltop in the Fb landscape.

Based on the results in the table I can state the first attempt at a criterion for success as the following:

• C1) If the rates of contraction for Fa around the attracting point and the rate of expansion for Fb around the saddle point are inversely proportional to each other, then a RNN can process the a^n b^n language by matching step sizes for "a" input and "b" input.

The above criterion explained how trajectory steps match in size, which helps explain how the network predicts the transition at the end of the string. However, it does not explain how a network can organize itself to so that the transition from the last "a" to the first "b" in an input sequence will put the network in a region of phase space such that the step sizes will match. I will explain this by looking at the eigenvectors at the saddle point.

Figure 13 replicates the vector flow field for Fb and Fb^2. I have also drawn in the lines in the direction of the eigenvectors, which intersect at the location of the saddle point. The line that crosses the HU2 axis near (0,.85) is the stable eigenvector line; and the line that crosses the HU2 axis near (0,.65) is the unstable eigenvector line. Values of {HU1,HU2} near the stable eigenvector get contracted in towards the saddle point before moving towards the periodic 2 fixed point. Notice that the attracting point for the Fa dynamics (see figure 12) nearly falls on the stable eigenvector line of the saddle point for the Fb dynamics. The full criterion can now be stated as follows:

• C2) If "C1)" above is satisfied, and if the attracting point of Fa lies on the stable eigenvector of the saddle point for Fb then a RNN can process the a^n b^n language.

These criteria describe coordinated trajectories.

6. CONCLUSION

The case 2 network generalized for n=16, which is 10 characters more in total string length than presented in training. The ability of the network to perform the task is manifested in the weight parameters of the output units and the dynamics of the hidden units. Although, the network did not generalize to an infinite length string, one can comfortably conjecture based on the analysis that the network dynamics reflect the structure of the input/output task.

In fact one can draw functional correspondences between the behavior of the network and the behavior of the PDA as follows:

          PDA:			RNN:
          stack/counter 		~ coordinated trajectories
          state 			~ region of activation values
          transition 		~ a change in activation values

I am not implying that a RNN is equivalent to a PDA; the coordinated trajectory concept I introduce is neither a stack nor a counter. However, in the context of the task domain and network architecture the hidden node dynamics realize an equivalent functional and informational content as that provided by a stack or counter in the context of a PDA. Also, the dynamical systems interpretation provides the correct functional description (as well as the mathematical analysis) of the resources employed by a RNN. In particular, a coordinated trajectory is composed of the following resources in the a^n b^n task domain: 1) the contracting dynamics of the attracting point under "a" input condition matches the expanding dynamics of the repelling point under the "b" input condition and 2) the attracting point under "a" input condition lies near the axis of convergence of the saddle point.

In conclusion, I can address the two questions I presented earlier: first, a RNN can learn to process a simple CFL; secondly the states and resources employed are correctly identified by a dynamical systems interpretation. A RNN can employ its resources to behave functionally as a stack/counter. However, there are important differences which may not correspond to a PDA. In the case of a PDA the states of the system that control the stack or counter is literally disconnected from the stack or counter device. In the case of a RNN one cannot decouple the coordinated trajectory from the states of the system. In fact, the trajectory is the state of activation values and the change of activation values.7

7. DISCUSSION

7.1 Overview

The work here has implications for a variety of issues. In this section I would like to briefly discuss some of these. My purpose is not to postulate any answers but rather point out that the work here adds a building block to the connectionist framework and perhaps new background information with which to frame some language processing questions.

7.2 The Psychological Account

An important question surrounding this work is the following: Does a RNN provide an alternative account of psychological data on human language processing than discrete automata? For example, a PDA with limitations on the stack depth can account for human performance limits on processing center-embedded sentences (Barton, et al. 1987). However, experiments have shown that semantic information might aid the processing of center-embedded sentences (Stolz, 1967). In a PDA framework this is problematic because syntactic processing constraints on the stack device must somehow depend on semantic constraints as well (Marcus, 1980). On the other hand, Weckerly and Elman (1992) have demonstrated that a RNN can learn to process center-embedded sentences with semantically biased verbs better than semantically unbiased verbs, suggesting that a RNN mechanism reflects some aspects of performance more seamlessly.

The work presented here suggests a related question that one can now ask: How does content affect trajectories? In other words, since we have some characterization of the resources involved in trajectories, we can begin to understand how different task domains, including ones that use semantic input, affects those resources. The affects could arise from precision, location of fixed points, rates of contraction/expansion, the topographical relationships of those axis of contraction/expansion, the ability of output units to "cut up" the phase space, etc.. The dynamical systems analysis presented here provides insight on some performance issues for RNN models of language processing, but by no means does it exhaust the possibilities.

7.3 Other Counters

Recently, Siegelmann has proved that one can construct a RNN to perform as counters (Siegelmann, 1993). Each counter consists of one linear node with only one recurrent connection to itself and the connections between nodes are laid out such that they only have limited interaction.

In my case 2 network the "counting up" values oscillate and converge around a fixed point, the "counting down" values oscillate and expand around a repelling fixed point. More importantly my network learned the solution, with hidden units that were fully connected to each other. The axis of expansion in case 2 contained components of both hidden units which suggests a solution that was distributed among units. The output units were not specially constructed but rather developed their own connection weights to cut up the hidden unit phase space as appropriate. In fact, since the output units were not connected to the input units the hidden layer was forced to find a solution that "counts up and down" in two different regions of phase space. Essentially, the case 2 network realizes a distributed solution for the task at hand.

7.4 What other CFLs can a RNN learn?

The possibility exists that the network dynamics are particular to the specific task and do not reflect the kind of dynamics needed for CFLs in general. For example, a more complicated CFL is the balanced parenthesis language.8 This language consists of some number of "a" and the same number of "b", but a "b" can be placed anywhere in the string such that it matches some previous "a". In other words, the "ab" can be embedding anywhere in the string. For this task the network can only correctly predict the end of the string.

Further testing of the case 2 network with strings from the balanced parenthesis language confirms that coordinated trajectories are sufficient to process other CFLs. For example, the case 2 network will correctly predict the transition at the end of strings such as "aabaabbb" and "aabaabaabbb". This result is striking because the network was never trained on any strings from the balanced parenthesis problem. The conditions to process this language are related to those for a^n b^n language. Future work will investigate whether or not a RNN can learn other CFLs. It is possible that the solution may involve a different set of dynamics or just dynamics that are more complex.

7.5 Constituent Structure

It is premature to fully compare a RNN with a PDA because a PDA is capable of producing output in the form of constituent-tree structure, which represents a hierarchical relationship of syntactic structure. A RNN trained on the prediction task can reflect structure of the input strings but it does not develop constituent structure representations. However, an appreciation of the RNN capabilities and limitations directed at addressing such issues will contribute to an understanding of possible syntactic machineries necessary to support the production and comprehension of language. This work has demonstrated that under some configuration of dynamics a RNN has capabilities that reflect the structure of the input, independent of string length.

ACKNOWLEDGEMENTS

I would like to thank Jeffrey Elman for excellent guidance and insightful discussions about everything herein, and Janet Wiles for providing some of her sample work and engaging discussions. Also, I benefited from very helpful feedback from John Batali, Michael Casey, Paul Minero, Mark St. John, and David Zipser.

BIBLIOGRAPHY

Batali, John (1994). "Innate Biases and Critical Periods: Combining Evolution and Learning in the Acquisition of Syntax". Proceedings of the Fourth Artificial Life Workshop, Cambridge, MA.

Casey, Michael Patrick (1995). Computation in Discrete-Time Dynamical Systems, Ph.D. dissertation, unpublished, University of California at San Diego.

Chalmers, David (1992). "Syntactic Transformations on Distributed Representations", in Connectionist Natural Language Processing, ed. Noel Sharkey, Kluwer Academic.

Elman, Jeffrey L. (1990). "Finding Structure in Time", in Cognitive Science 14, Ablex.

Elman, Jeffrey L. (1991). "Distributed Representations, Simple Recurrent Networks, and Grammatical Structure" in Machine Learning 7, Kluwer Academic.

Giles, C.L., Sun, G.Z., Chen, H.H., Lee, Y.C., Chen, D. (1992) "Extracting and Learning and Unknown Grammar with Recurrent Neural Networks" in Advances in Information Processing 4, J.E. Moody, S.J. Hanson and R.P. Lippmann (eds), Morgan Kaufman, San Mateo, Ca.

Giles, C. Lee, and Omlin, Christian W. (1993). "Extraction, Insertion and Refinement of Symbolic Rules in Dynamically Driven Recurrent Neural Networks", in Connection Science, Vol5, Nos. 3 and 4.

Hopcroft, John E., and Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages, and Computation, Addison-Wesley.

Kwasny, Stan C., and Kalman, Barry L. (1995). "Tail-recursive Distributed Representations and Simple Recurrent Networks", in Connection Science, Vol7, No 1.

Lucas, S. M., Damper, R. I. (1992). "Syntactic Neural Networks", in Connectionist Natural Language Processing, ed. Noel Sharkey, Kluwer Academic.

Marcus, Mitchell P., (1980). A Theory of Syntactic Recognition for Natural Language, MIT Press, Cambridge, Mass..

Miikulainen, Risto (1992). "Script Recognition with Hierarchical Feature Maps", in Connectionist Natural Language Processing, ed. Noel Sharkey, Kluwer Academic.

Maskara, Arun and Noetzel, Andrew (1992) "Sequence Recogntion withRecurrent Neural Networks", Technical Report, New Jersey Institute of Technology.

McClelland, James L., and Kawamoto, Alan H. (1986). "Mechanisms of Sentence Processing: Assigning Roles to Constituents", in Parallel Distributed Processing Vol. 1, MIT Press.

Rumelhart, D. E., Hinton, G.E., Williams, R.J. (1987). "Learning Internal Representations by Error Propagation", in Parallel Distributed Processing Vol. 1, MIT Press.

Servan-Schreiber, David, Cleermans, Axel, and McClelland, James L. (1988) "Encoding Sequential Structure in Simple Recurrent Networks", CMU Technical Report CS-88-183.

Siegelmann, Hava Tova (1993). Foundations of Recurrent Neural Networks, Ph.D. dissertation, unpublished. New Brunswick Rutgers, The State University of New Jersey.

Smith, Anthony W. and Zipser, David (1989). "Learning Sequential Structure with the Real-Time Recurrent Learning Algorithm", International Journal of Neural Systems, Vol.1, No. 2.

St John, Mark (1992). "The Story Gestalt: A Model of Knowledge-Intensive Processes in Text Comprehension", Cognitive Science, 16.

Stolcke, Andreas (1990). "Learning Feature-Based Semantics with Simple Recurrent Networks", Technical Report, ICSI, UC Berkeley.

Stolz, W.S. (1967). "A Study of the Ability to Decode Grammatically Novel Sentences", in Journal of Learning and Verbal Behavior, Vol. 6.

Sun, G.Z., Chen, H.H., Giles, C.L., Lee, Y.C., Chen, D. (1990). "Connectionist Pushdown Automata That Learn Context-Free Grammars", in IJCNN, Washington D.C.

Tino, Peter, Horne, Bill, and Giles, Lee (1995). "Finite State Machines and RecurrentNeural Networks - Automata and Dynamical Systems Approaches", Technical Report-UMCP-CSD:CS-TR-3396, University of Maryland, College Park.

Watrous, Raymond L., and Kuhn, Gary M. (1992). "Induction of Finite-State Automata Using Second Order Recurrent Networks" in Advances in Information Processing 4, J.E. Moody, S.J. Hanson and R.P. Lippmann (eds), Morgan Kaufman, San Mateo, Ca.

Weckerley, Jill and Elman, Jeffrey L. (1992). "A PDP Approach to Processing Center-Embedded Sentences", in Proceedings of the Fourteenth Annual Conference of the Cognitive Science Society, Indiana University, Bloomington, Lawrence Erlbaum Associates, Hillsdale, N.J.

Williams, Ronald J., and Zipser, David (1989). "Experimental Analysis of the Real-Time Recurrent Learning Algorithm", in Connection Science, Vol. 1, No. 1.

1 Several works have demonstrated that feed-forward networks are capable of representing complex structural relationships, such as the RAAM model (e.g. Chalmers, 1992). Also, there have been other works showing that feed-forward networks are capable of performing semantic processes, such as assigning thematic role information (McClelland and Kawamoto, 1986; Miikkulainen, 1992). Some researches have built networks to handle temporal structure by using special delay lines or hierarchical structure (Lucas and Damper, 1992). My emphasis here is on networks that attempt to organize itself to match the temporal structure of the language task.

2 Note that the phase space diagram does not include an axis for time.

3 An eigenvalue is a scalar (, and an eigenvector is a vector v, such that for a system of equations F, Fv=(v.

4 The case 1 network did not actually have a repelling point, however, I used the point that had the smallest change in activation values, which still allows one to make a rough comparison of dynamics.

5 Case 3 had dynamics that monotonically increase for 1 hidden unit in Fa, then monotonically decreased for the other hidden unit in Fb, but in this case the dynamics have a repelling point.

6 The other eigenvalues are only important in the sense that they are small enough so that the larger eigenvalues "dominate" the action.

7 This claim is supported by formal definitions. In the set theoretic language of automata the stack or counter is a discrete set distinct from the set of control states. In the set theoretic language of dynamical systems a trajectory (or orbit) is the real-valued set of state variables through time.

8 In fact the language a^n b^n is a subset of the balanced parenthesis language.